Anemômetros são instrumentos usados para medir a velocidade do vento. A sua construção mais conhecida é a proposta por Robinson em 1846, que consiste em um rotor com quatro conchas hemisféricas presas por hastes, conforme figura abaixo. Em um anemômetro de Robinson ideal, a velocidade do vento é dada pela velocidade linear das conchas. Um anemômetro em que a distância entre as conchas e o centro de rotação é r = 25 cm, em um dia cuja velocidade do vento é v = 18 km/h, teria uma frequência de rotação de

Se necessário, considere π ≈ 3.
A relação entre velocidade linear e velocidade angular é:

Do enunciado, tem-se:

Efetuadas as devidas substituições:
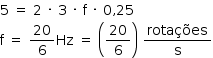
Essa frequência, expressa em  (rpm), é:
(rpm), é:
