Músculos artificiais feitos de nanotubos de carbono embebidos em cera de parafina podem suportar até duzentas vezes mais peso que um músculo natural do mesmo tamanho. Considere uma fibra de músculo artificial de 1 mm de comprimento, suspensa verticalmente por uma de suas extremidades e com uma massa de 50 gramas pendurada, em repouso, em sua outra extremidade. O trabalho realizado pela fibra sobre a massa, ao se contrair 10%, erguendo a massa até uma nova posição de repouso, é
Se necessário, utilize g = 10 m/s2.
A situação descrita pelo enunciado pode ser esquematizada como segue:
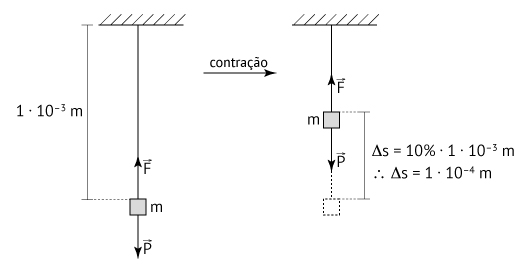
Considerando que a força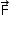 
que a fibra aplica no corpo equilibre o peso 
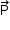do corpo durante a contração da fibra, podemos calcular o trabalho 
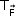dessa força como segue:
