Um caminhão carregando uma caixa trafega em linha reta a uma velocidade de 36 km/h. O coeficiente de atrito estático entre a superfície da caixa e a superfície da carroceria é de 0,4 e não há ganchos ou amarras prendendo a caixa ao caminhão. Sabendo disso e ao notar um sinal vermelho à frente, o motorista freia suavemente o caminhão para que a caixa não deslize.
a) Desenhe um diagrama de corpo livre indicando as forças que atuam sobre a caixa durante a frenagem.
b) Calcule a distância mínima que o caminhão percorre entre o instante de início da frenagem e a parada total do veículo para que a caixa permaneça sem deslizar.
c) Se o motorista frear totalmente o caminhão em 1,5 s, a caixa deslizará na carroceria? Justifique.
Note e adote:
Considere que a força exercida pelos freios do caminhão seja feita de modo que a aceleração do caminhão seja constante durante a frenagem. Aceleração da gravidade: g = 10 m/s2
a) O diagrama de corpo livre pode assim ser representado:
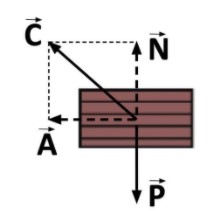
Sendo:
: Peso;
: Componente normal da força de contato;
: Componente atrito da força de contato;
: Força de contato.
b) Como o movimento é horizontal, a resultante apresenta apenas componente nessa direção, logo:
A distância mínima que o caminhão percorre ocorre quando a caixa está na iminência de escorregamento.
Utilizando a equação de Torricelli:
c) Calculando a distância percorrida no intervalo de tempo dado:
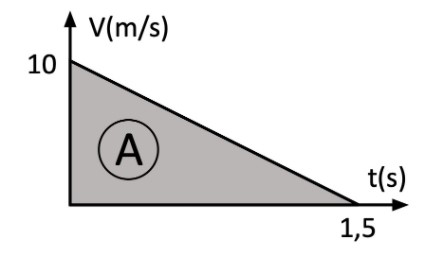
Como , conclui-se que a caixa vai escorregar (deslizar na carroceria).