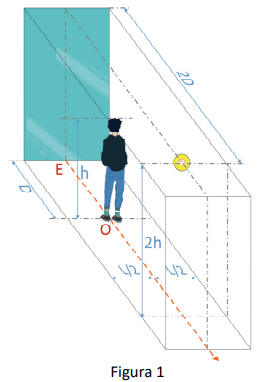
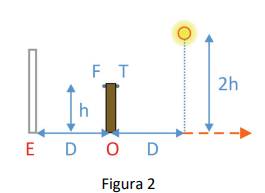
Uma pessoa de altura h posiciona-se de pé em um quarto vazio, no qual três das quatro paredes são escuras, enquanto a parede restante é um espelho quase perfeito. O quarto é iluminado por uma única lâmpada, aproximadamente esférica e situada a uma altura 2h. A figura 1 mostra uma vista superior, e a figura 2, uma vista lateral do quarto. Na figura 2, “O” indica a posição da pessoa e “E”, a posição do espelho. As dimensões da lâmpada são muito menores que os demais comprimentos relevantes. Nessas condições, são formadas duas sombras da pessoa no piso do quarto. Na folha de resposta, há diagramas nos quais o círculo representa a pessoa e os tons mais claros/escuros indicam uma sombra menos/mais intensa.
a) Dentre os diagramas, indique aquele que melhor corresponde ao padrão de sombras que, na situação descrita, seria observado na sala.

b) Determine os comprimentos das sombras considerando os dados fornecidos.
A intensidade da radiação luminosa é definida como a energia luminosa transportada por unidade de área por unidade de tempo. Para fontes luminosas esféricas pontuais, a intensidade luminosa em um certo ponto deve diminuir com o inverso do quadrado da distância do ponto à fonte luminosa.
c) Desprezando as dimensões da cabeça da pessoa em relação aos demais comprimentos relevantes, tomando h = D e supondo que não haja reflexão relevante da luz em qualquer outra superfície que não a parede espelhada, determine a razão numérica entre a intensidade luminosa no ponto F e aquela no ponto T, localizados na cabeça da pessoa e indicados na figura 2.
a) Desprezando a distância : pode-se construir o esquema óptico representado na figura 1, onde está representada a construção da sombra AO.
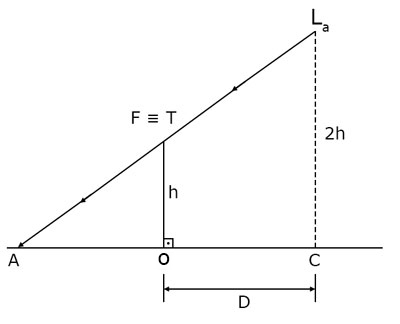
Figura 1
Como :
O raio de luz que parte da lâmpada, e passa pelo ponto “F”, atinge o ponto “A” a uma distância D do ponto “O”. Assim, o ponto “A” coincide com o ponto “E”, como indicado no esquema óptico apresentado na figura 2. Nesse esquema óptico, também está apresentada a construção da sombra OB. Note que La’ é a imagem da lâmpada La formada pelo espelho plano.
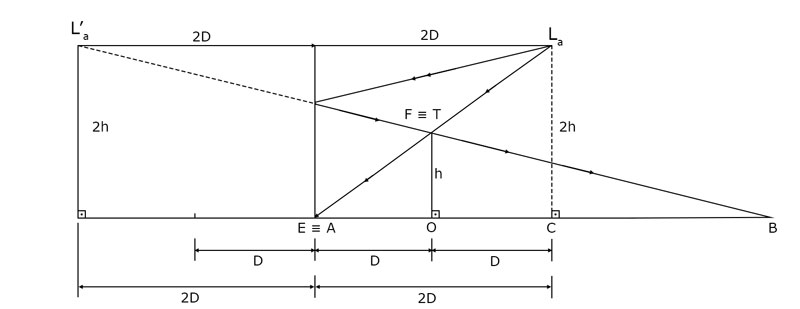
Figura 2
A partir da figura, observamos que . Além disso, observa-se que a região da sombra OB é mais iluminada que a da sombra AO. Assim, o diagrama que melhor corresponde ao padrão de sombras é o diagrama 2.

b) A partir do item "a":
Da figura 2:
Ainda na figura . Assim,
c) De acordo o enunciado, a intensidade luminosa é inversamente proporcional ao quadrado da distância, portanto:
sendo k a constante de proporcionalidade.
A partir da figura 2, verifica-se no item “a” que e
. Dessa forma,
Assim, a intensidade luminosa no ponto “T”, IT, é dada por
Para se determinar a intensidade luminosa no ponto “F”, IF, primeiro deve-se calcular a distância percorrida pela luz que parte da lâmpada, reflete no espelho e atinge o ponto “F”. Essa distância é igual a , indicada na figura 2. Assim,
A figura 2,
Dessa forma:
A intensidade IF é dada por
Assim, pode-se calcular a razão numérica :