Um modelo simplificado de uma panela de pressão consiste em um recipiente cilíndrico provido de uma tampa com borda emborrachada que previne a saída de vapor. No centro da tampa, sobre um orifício de área A, repousa uma válvula de massa m que pode se deslocar verticalmente, sem atrito, e que impede que a pressão P interna à panela ultrapasse um valor limite. A pressão atmosférica e a aceleração da gravidade no local de operação da panela são, respectivamente, P0 e g.
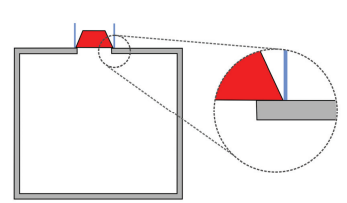
a) Liste todas as forças que atuam verticalmente sobre a válvula num instante em que ela está em perfeito contato com a tampa da panela.
b) Deseja-se que a panela atinja uma pressão interna de operação não inferior a 2P0. Por outro lado, os materiais de que é feita a panela são capazes de suportar uma pressão interna máxima igual a 3,5P0, além da qual a panela explode. Qual deve ser a faixa de valores da massa m da válvula para que a panela funcione segundo as especificações?
c) Suponha que a panela, vedada, esteja sobre a chama do fogão e que seu interior esteja completamente ocupado por uma mistura de ar com vapor de água, totalizando N mols de gás que pode ser considerado ideal. Nesse momento, a pressão interna é P1, e a energia cinética média das moléculas no gás é E1. Ao longo de mais algum tempo, com a panela ainda perfeitamente vedada, a chama do fogão transfere energia para o gás e eleva a energia cinética média das moléculas para um valor E2, que é 10% maior do que E1. Determine a razão entre o valor P2 da pressão interna nesse instante final e seu valor inicial P1.
Note e adote:
Considere que a área de contato entre a válvula e os seus pontos de apoio na panela é desprezível frente à área A.
a) As forças que atuam verticalmente sobre a válvula em contato com a panela estão representadas na figura abaixo:
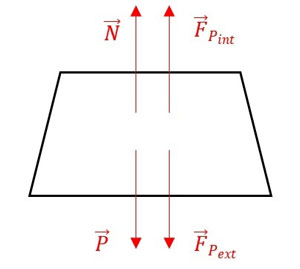
Onde:
: normal
: peso
: força de pressão interna
: força de pressão externa (atmosférica)
b) Com o aquecimento da panela, a força de pressão interna aumenta, diminuindo a normal. A partir do momento em que a válvula perde o contato com a panela (N = 0), parte do vapor vai sendo liberado, e a pressão interna passa a ser constante. Assim, no equilíbrio, temos:
Dividindo pela área (A) membro a membro, obtemos:
As massas mínima e máxima da válvula serão obtidas a partir das pressões internas mínima e máxima. Assim, temos:
Logo:
c) A energia cinética média das moléculas do gás é diretamente proporcional à temperatura absoluta do gás:
(1)
(2)
Como E2 é 10% maior do que E1, temos:
(3)
Substituindo as equações (1) e (2) em (3):
Aplicando a equação de Clapeyron aos estados 1 e 2 e dividindo membro a membro, temos: