Um plano de inclinação θ situa-se sobre uma mesa horizontal de altura 4h, conforme indicado na figura. Um carrinho de massa m parte do repouso no ponto A, localizado a uma altura h em relação à superfície da mesa, até atingir o ponto B na parte inferior do plano para então executar um movimento apenas sob a ação da gravidade até atingir o solo a uma distância horizontal D da base da mesa, conforme mostra a figura. Ao utilizarmos rampas com diferentes inclinações θ (com o carrinho sempre partindo de uma mesma altura h), obtemos diferentes alcances horizontais D.
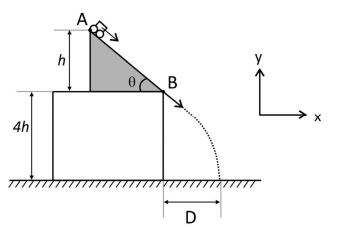
a) Calcule o intervalo de tempo decorrido entre a partida do carrinho, situado inicialmente no topo do plano inclinado, até atingir o solo, considerando o valor para a inclinação θ = 90°.
b) Usando a conservação da energia mecânica e supondo agora uma inclinação θ qualquer, obtenha o módulo do vetor velocidade com que o carrinho deixa a superfície do plano inclinado.
c) Encontre o valor do alcance D supondo que a inclinação do plano seja de θ = 45°.
Note e adote:
Considere conhecido o módulo g da aceleração da gravidade. Despreze o efeito de forças dissipativas.
a) Como θ = 90°, a distância entre A e B é “h”. Assim sendo, podemos considerar que o carrinho executa queda livre (movimento uniformemente variado) de uma altura total de “5h”. Logo:
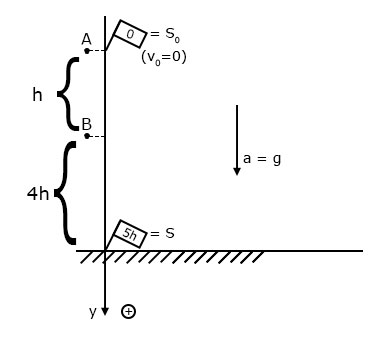
b) O carrinho, durante seu movimento sobre o plano inclinado, é um sistema conservativo, logo, sua energia mecânica permanece constante.
c) Determinando as componentes da velocidade () do carrinho no instante que ele perde o contato com o apoio, temos:
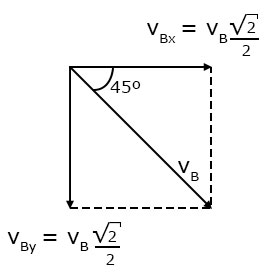
Na direção vertical, o movimento é uniformemente variado, logo, podemos calcular o tempo de queda da seguinte forma:
Resolvendo a equação do 2º grau, ,
,
:
Logo:
Assim: ou
.
Na direção horizontal, o movimento é uniforme, logo: