Considere a função f:  começar estilo tamanho matemático 14px reto números reais seta para a direita reto números reais fim do estilo dada por f(x) = p + q cos(rx - s), em que p, q, r e s são números reais e o cosseno é calculado sobre valores em radianos.

a) Qual é o valor máximo de f para o caso em que p=q=r=s1?

b) Quais são os valores do período e da amplitude de f, para o caso em que p = −1, q = 2, r = π e s = 0?

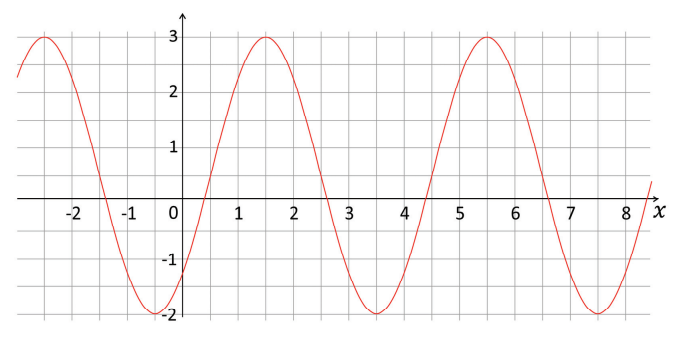
c) Determine valores de p, q, r e s no caso em que o gráfico de f é igual ao mostrado na figura a seguir. 

Note e adote:
A amplitude de uma função é a diferença entre seus valores máximo e mínimo.
O gráfico apresentado refere-se somente ao item (c).

a) começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço 1 espaço mais espaço cos espaço parêntese esquerdo reto x espaço menos espaço 1 parêntese direito fim do estilo
Como o valor máximo de cos (x – 1) é 1, o valor máximo de f(x) é 2.

b) começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço menos 1 espaço mais espaço 2 vezes cos espaço parêntese esquerdo πx parêntese direito fim do estilo
O período de f é dado por começar estilo tamanho matemático 14px numerador 2 reto pi sobre denominador linha vertical reto pi linha vertical fim da fração espaço igual a espaço 2 fim do estilo.
O valor máximo de f(x) é dado por –1 + 2 · 1 = 1.
O valor mínimo de f(x) é dado por –1 + 2 · (–1) = –3.
A amplitude é dada por 1 – (–3) = 4.
Logo, o período é 2 e a amplitude é 4.

c) começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço reto p espaço mais espaço reto q vezes cos espaço parêntese esquerdo rx espaço menos espaço reto s parêntese direito fim do estilo
O valor máximo de f(x) é 3 e seu valor mínimo é –2.
O valor de p é dado por começar estilo tamanho matemático 14px numerador 3 espaço mais parêntese esquerdo menos 2 parêntese direito sobre denominador 2 fim da fração espaço igual a espaço 1 meio fim do estilo.
Assim, tem-se que:
começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço 1 meio espaço mais espaço reto q vezes cos espaço parêntese esquerdo rx espaço menos espaço reto s parêntese direito fim do estilo
Como os valores extremos de cos (rx – s) são 1 e –1 e considerando os valores máximo e mínimo de f(x), conclui-se que começar estilo tamanho matemático 14px reto q espaço igual a espaço 5 sobre 2 fim do estilo ou começar estilo tamanho matemático 14px reto q espaço igual a espaço menos 5 sobre 2 fim do estilo.
Logo, começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço 1 meio espaço mais espaço 5 sobre 2 vezes cos espaço parêntese esquerdo rx espaço menos espaço reto s parêntese direito fim do estilo ou começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço 1 meio espaço menos espaço 5 sobre 2 vezes cos espaço parêntese esquerdo rx espaço menos espaço reto s parêntese direito fim do estilo.
Em ambos os casos, sendo r ≠ 0, o período de f(x) é dado por começar estilo tamanho matemático 14px numerador 2 reto pi sobre denominador linha vertical reto r linha vertical fim da fração fim do estilo.
Pelo gráfico, pode-se concluir que o período é 4.
De começar estilo tamanho matemático 14px 4 espaço igual a espaço numerador 2 reto pi sobre denominador linha vertical reto r linha vertical fim da fração fim do estilo, tem-se começar estilo tamanho matemático 14px linha vertical reto r linha vertical espaço igual a espaço reto pi sobre 2 fim do estilo, ou seja, começar estilo tamanho matemático 14px reto r espaço igual a espaço reto pi sobre 2 fim do estilo ou começar estilo tamanho matemático 14px reto r espaço igual a espaço menos reto pi sobre 2 fim do estilo.
Vamos considerar, inicialmente, os casos com p, q e r positivos.

começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço 1 meio espaço mais espaço 5 sobre 2 vezes cos espaço abre parênteses reto pi sobre 2 reto x espaço menos espaço reto s fecha parênteses fim do estilo

De começar estilo tamanho matemático 14px reto f abre parênteses 3 sobre 2 fecha parênteses espaço igual a espaço 3 fim do estilo, tem-se:

começar estilo tamanho matemático 14px 1 meio espaço mais espaço 5 sobre 2 vezes cos espaço abre parênteses reto pi sobre 2 vezes 3 sobre 2 espaço menos espaço reto s fecha parênteses espaço igual a espaço 3 cos espaço abre parênteses reto pi sobre 2 vezes 3 sobre 2 espaço menos espaço reto s fecha parênteses espaço igual a espaço 1 numerador 3 reto pi sobre denominador 4 fim da fração espaço menos espaço s espaço mais espaço 2 h reto pi espaço igual a espaço 0 reto s espaço igual a espaço numerador 3 reto pi sobre denominador 4 fim da fração espaço mais espaço 2 hπ espaço espaço parêntese esquerdo sendo espaço reto h espaço um espaço inteiro espaço qualquer parêntese direito fim do estilo

No caso mais simples, tem-se começar estilo tamanho matemático 14px reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço 1 meio espaço mais espaço 5 sobre 2 vezes cos espaço abre parênteses reto pi sobre 2 reto x espaço menos espaço numerador 3 reto pi sobre denominador 4 fim da fração fecha parênteses fim do estilo. 
Nesse caso, tem-se começar estilo tamanho matemático 14px reto p espaço igual a espaço 1 meio fim do estilo, começar estilo tamanho matemático 14px reto q espaço igual a espaço 5 sobre 2 fim do estilo, começar estilo tamanho matemático 14px reto r espaço igual a espaço reto pi sobre 2 fim do estilo e começar estilo tamanho matemático 14px reto s espaço igual a espaço numerador 3 reto pi sobre denominador 4 fim da fração fim do estilo.
Porém há muitos outros casos a serem considerados.
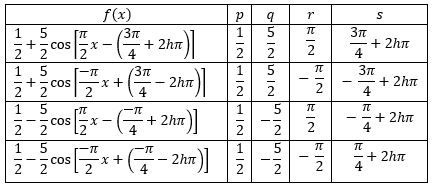
Sendo h um número inteiro qualquer, tem-se a seguinte tabela de casos possíveis.