O perímetro de uma figura plana é o comprimento de seu contorno. O diâmetro de uma figura plana é a maior distância entre dois pontos do contorno dessa figura. Calcule a razão entre o perímetro e o diâmetro em cada uma das figuras planas nos casos a seguir:
a) Um retângulo com lados de medidas 3 e 4.
b) O triângulo obtusângulo ABC mostrado na Figura 1.
c) A região colorida dentro do círculo de raio r mostrada na Figura 2.

a) Observe a figura:

Da figura, tem-se que o perímetro do retângulo vale 3 + 3 + 4 + 4 = 14, e o diâmetro é dado pelo comprimento de uma das diagonais do retângulo. No triângulo retângulo ACD, pelo teorema de Pitágoras, vem que AD = 5 e, assim, a razão pedida vale
b) Observe a figura:
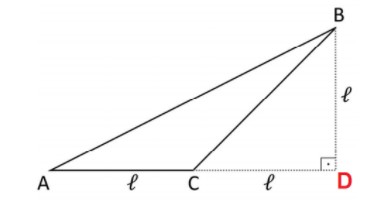
Aplicando o teorema de Pitágoras ao triângulo retângulo BCD, obtém-se e aplicando o teorema de Pitágoras ao triângulo retângulo BAD, vem que
e, assim,
Logo, o perímetro do triângulo vale
, e seu diâmetro (o comprimento do segmento
) vale
, de modo que a razão pedida vale
=
.
c) Observe a figura:
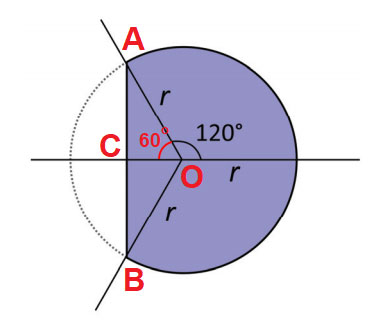
Admitindo que a corda da circunferência de centro O e raio com medida r seja perpendicular à reta
, tem-se, no triângulo retângulo ACO, que
e, assim, . Uma vez admitida a hipótese citada anteriormente, a figura possui simetria axial, sendo
o eixo de simetria. Com isso, o perímetro dessa figura é dado pela soma de AB com o comprimento de um arco de circunferência cujo ângulo central mede 120° + 120° = 240° e raio com medida r e vale .
Como o diâmetro dessa figura vale 2r, a razão pedida é dada por .