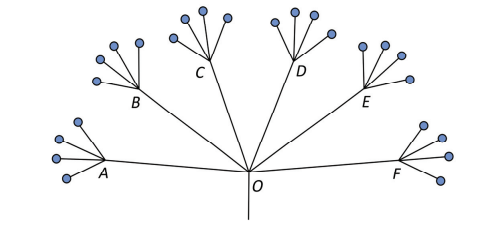
Um parque industrial com 24 indústrias foi estruturado de forma que seu sistema de esgoto tivesse a estrutura mostrada na figura. Um serviço de inspeção no ponto O detectou uma substância proibida que pode ter vindo de qualquer uma das indústrias, com igual probabilidade. Para autuar as indústrias irregulares, o serviço se decidiu pela seguinte estratégia: usar 6 kits de teste em amostras coletadas nos pontos A, B, C, D, E e F, no primeiro dia e, no segundo dia, fazer o mesmo nas saídas de todas as indústrias dos grupos apontados como contaminados no primeiro dia. Um dos cenários examinados pelo serviço de inspeção foi o de haver exatamente quatro indústrias irregulares.
a) Quantas são as formas possíveis de exatamente quatro indústrias irregulares estarem distribuídas entre as 24 indústrias do parque?
b) Qual é a probabilidade, havendo exatamente quatro indústrias irregulares, de que o gasto total de kits de testes nos dois dias seja 22?
c) Qual é a probabilidade, havendo exatamente quatro indústrias irregulares, de que o gasto total de kits de testes usados nos dois dias seja 14 ou menos?
a) Dado que há 24 indústrias no parque, admitindo que há exatamente 4 indústrias irregulares, e que se a escolha das indústrias irregulares não depende da ordem, isto é, escolher A1, A2, A3 e A4 é equivalente a escolher A4, A1, A2 e A3, tem-se que o total de possibilidade é dado por:
b) Tendo exatamente quatro indústrias irregulares, tem-se os seguintes cenários:
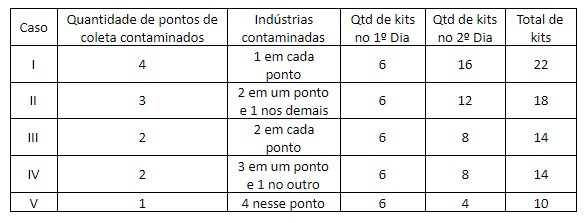
OBS.: Mesmo não sendo necessário fazer a segunda rodada de testes no caso V, o enunciado deixa claro que ela será feita. Caso não fosse realizada a segunda rodada, teríamos apenas 6 kits no total. Isso não influenciará a probabilidade pedida.
Nota-se que o único caso em que o total de kits foi de 22 é o I. Assim, pode-se resolver o problema dos seguintes modos:
Modo I
A quantidade de maneiras de escolher 4 pontos de coleta dentre os 6 é dada por
Escolhidos os pontos de coleta, tem-se 4 indústrias para serem escolhidas em cada ponto de coleta. Assim, a quantidade de maneiras de realizar essa escolha é dada por 4 · 4 · 4 · 4.
Com isso, o número de casos favoráveis é dado por . E assim, a probabilidade desse caso acontecer é de:
Modo II
- Na escolha da primeira indústria, não há restrição, isto é, qualquer uma das 24 indústrias pode ser escolhida. A probabilidade disso é de
.
- Na escolha da segunda indústria, restaram 20 casos favoráveis (não se pode escolher nem a já escolhida no passo anterior, tampouco as outras 3 do mesmo ponto de coleta) em um total de 23 (retiramos apenas a escolhida no passo anterior). Sendo assim, a probabilidade é de
.
- Analogamente, na escolha da terceira indústria restaram 16 casos favoráveis em um total de 22. Sendo assim, a probabilidade é de
.
- Analogamente, na escolha da quarta indústria restaram 12 casos favoráveis em um total de 21. Sendo assim, a probabilidade é de
.
Com isso, a probabilidade solicitada é dada por
c) Para obter 14 kits ou menos, tem-se os casos III, IV e V. Avaliando cada um deles de acordo com o Modo I utilizado no item b, tem-se:
Caso III
A quantidade de maneiras de escolher 2 pontos de coleta dentre os 6 (cada um deles com a mesma quantidade de indústrias contaminadas) não depende da ordem de escolha, sendo assim, tem-se um total de .
Escolhidos os pontos de coleta, tem-se que escolher 2 indústrias de cada ponto de coleta, dentre as quatro possibilidades. Como a ordem é irrelevante, tem-se maneiras de escolher as indústrias para cada ponto.
Com isso, o número de casos favoráveis é dado por .
Caso IV
Como nesse caso a quantidade de indústrias contaminadas em cada ponto de coleta é diferente, tem-se que a ordem de escolha é relevante. Escolhendo um dos 6 pontos e três indústrias contaminadas, tem-se um total de .
Escolhendo um dos cinco pontos e escolhendo uma indústria contaminada, tem-se .
Com isso, o número de casos favoráveis é dado por 6 · 4 · 5 · 4.
Caso V
Tem-se que escolher 1 ponto de coleta, dentre os 6. E, escolher 4, dentre as 4 indústrias. Isso pode ser feito de .
Com isso, o número de casos favoráveis é dado por:
E assim, a probabilidade de esse evento acontecer é de: