A figura indica uma sequência de polígonos regulares com número n par de lados, cada um medindo 2 cm. Cada polígono tem um lado sobre a reta r e o lado oposto sobre uma reta paralela a r. Estas retas paralelas a r estão indicadas por t1, t2, t3,....
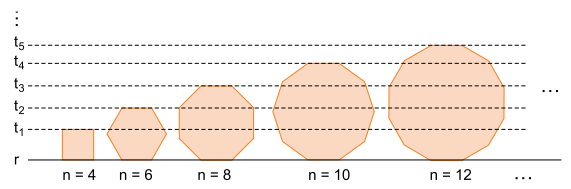
a) Calcule a distância entre as retas t1 e t2.
b) Mantendo-se o padrão da sequência, calcule a distância entre as retas t23 e t24 em função de letras convenientemente selecionadas da tabela.
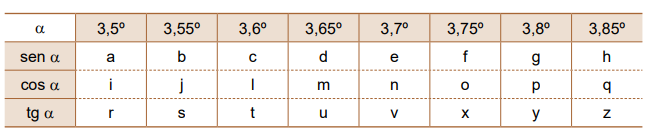
a) Observe a figura:
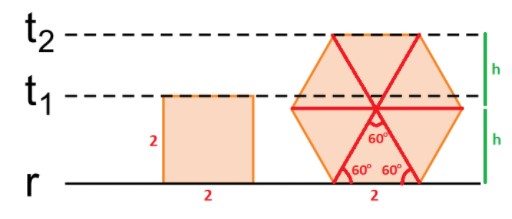
A distância entre as retas r e t1 é igual à medida do lado do quadrado e vale 2.
Como todo hexágono regular pode ser dividido em 6 triângulos equiláteros congruentes entre si, a distância entre as retas r e t2 pode ser obtida fazendo-se 2 vezes a altura h de um triângulo equilátero com lado medindo 2. Assim, como , tem-se que essa distância vale
.
Logo, a distância entre t1 e t2 vale .
b) A figura abaixo representa um polígono regular A1A2...An com n lados, todos medindo 2 cm e o ângulo central de medida :
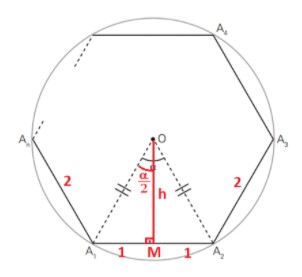
Sendo h a altura do triângulo isósceles OA1A2, no triângulo retângulo OMA1, tem-se:
Além disso, como , é possível escrever
. (*)
Da figura dada no enunciado, note que a distância entre as retas r e ti vale o dobro da altura h obtida em (*).
Agora, observe a seguinte correspondência:

Assim, conclui-se que:
- a distância entre r e t23 vale
;
- a distância entre r e t24 vale
;
- a distância entre t23 e t24 vale
.