Em um plano cartesiano de origem A = (0, 0) foram desenhados os quadrados ABCD, DEFG e HIJD. Sabe-se que B = (0, 5), G = (8, 0), H pertence ao eixo das abscissas, J está na intersecção de com
e λ é uma circunferência que passa por B, C e G, como mostra a figura.
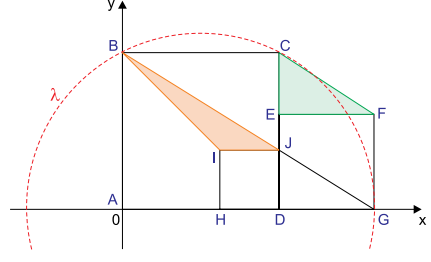
a) Determine as áreas dos triângulos CEF e JIB, em unidades de área do plano cartesiano.
b) Determine as coordenadas do centro de λ e seu raio.
a) Como B(0,5) e G(8,0), então o quadrado ABCD tem lado medindo 5 e, assim, D(5,0) e C(5,5). Além disso, como AG = 8 e AD = 5, tem-se DG = 3 e, portanto, o lado do quadrado DEFG mede 3. Dessa forma, EF = 3 e CE = CD – ED = 5 – 3 = 2. Logo, a área do triângulo CEF vale .
A partir da semelhança entre os triângulos JDG e BAG, é possível escrever:
Portanto, o lado do quadrado HIJD mede e, assim,
. Logo, a área do triângulo BIJ vale
.
b) Denotando por C(a,b) as coordenadas do centro da circunferência e R a medida do raio, como a circunferência contém os pontos (0,5), (5,5) e (8,0), é possível escrever:
Igualando (I) e (II), obtém-se:
Igualando (II) e (III), com :
Substituindo e
em (I), obtém-se:
As coordenadas do centro são e o raio mede
.