Considere o guindaste mostrado nas figuras, em duas posições (1 e 2). Na posição 1, o braço de movimentação forma um ângulo reto com o cabo de aço CB que sustenta uma esfera metálica na sua extremidade inferior.
Na posição 2, o guindaste elevou seu braço de movimentação e o novo ângulo formado entre o braço e o cabo de aço ED, que sustenta a bola metálica, é agora igual a 60°.
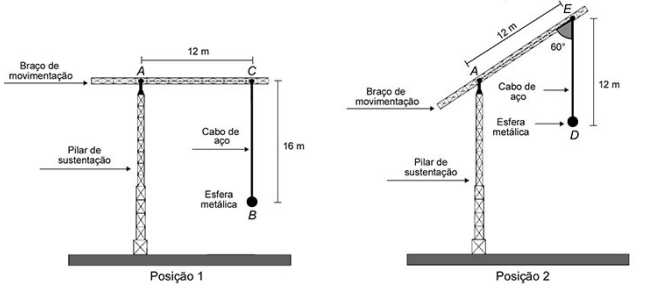
Assuma que os pontos A, B e C, na posição 1, formam o triângulo T1 e que os pontos A, D e E, na posição 2, formam o triângulo T2, os quais podem ser classificados em obtusângulo, retângulo ou acutângulo, e também em equilátero, isósceles ou escaleno.
Segundo as classificações citadas, os triângulos T1 e T2 são identificados, respectivamente, como
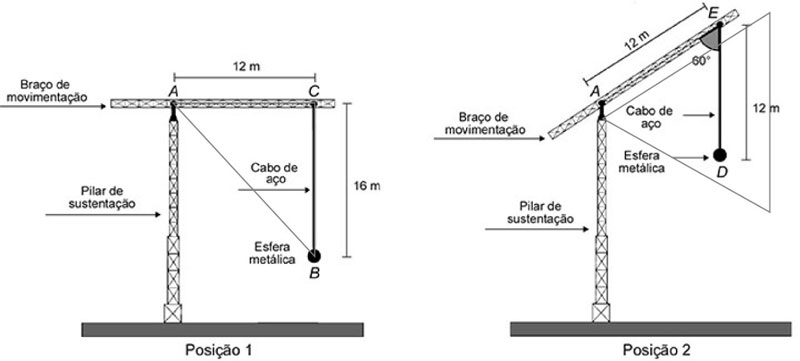
Na Posição 1, o triângulo ABC é retângulo em C. Aplicando o teorema de Pitágoras, tem-se que AB = 20 m, como os três lados são desiguais (12 m, 16 m e 20 m), ABC é retângulo escaleno.
Na Posição 2, temos AE = ED = 12 m e o ângulo AÊD mede 60°. Logo, os ângulos EAD e EDA também medem 60° , assim, ADE é triângulo acutângulo equilátero.