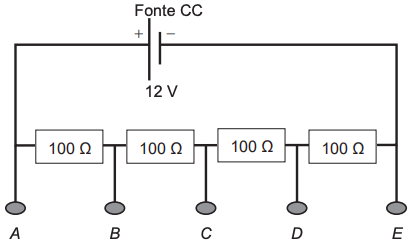
Um estudante tem uma fonte de tensão com corrente contínua que opera em tensão fixa de 12 V. Como precisa alimentar equipamentos que operam em tensões menores, ele emprega quatro resistores de 100 Ω para construir um divisor de tensão. Obtém-se este divisor associando os resistores, como exibido na figura. Os aparelhos podem ser ligados entre os pontos A, B, C, D e E, dependendo da tensão especificada.
Ele tem um equipamento que opera em 9,0 V com uma resistência interna de 10 kΩ.
Entre quais pontos do divisor de tensão esse equipamento deve ser ligado para funcionar corretamente e qual será o valor da intensidade da corrente nele estabelecida?
Como os resistores do circuito apresentam a mesma resistência elétrica, a tensão da fonte é igualmente dividida entre cada dois pontos consecutivos. Assim:
Considerando que o equipamento que será ligado ao circuito fornecido é um resistor e sendo sua resistência com ordem de grandeza maior que as resistências de 100 Ω, pode-se admitir que, ao ligar o equipamento entre os pontos convenientes, não há alteração na d.d.p. entre os pontos A, B, C, D e E.
Dessa forma, para que a tensão no equipamento seja 9 V, deve-se ligá-lo entre os pontos AD ou BE. Portanto, elimina-se as alternativas A e E.
Ligando o equipamento de forma conveniente, pode-se assim obter a corrente elétrica que nele se forma:
Descarta-se assim as alternativas B e C e assinala-se a alternativa D.