Ondas estacionárias podem ser produzidas de diferentes formas, dentre elas esticando-se uma corda homogênea, fixa em dois pontos separados por uma distância L, e pondo-a a vibrar. A extremidade à direita é acoplada a um gerador de frequências, enquanto a outra extremidade está sujeita a uma força tensional produzida ao se pendurar à corda um objeto de massa m0 mantido em repouso. O arranjo experimental é ilustrado na figura. Ajustando a frequência do gerador para f1, obtém-se na corda uma onda estacionaria que vibra em seu primeiro harmônico.
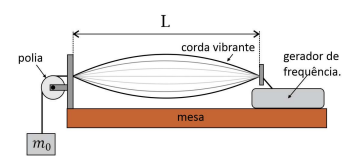
Ao trocarmos o objeto pendurado por outro de massa M, observa se que a frequência do gerador para que a corda continue a vibrar no primeiro harmônico deve ser ajustada para 2f1. Com isso, é correto concluir que a razão M/m0 deve ser:
Quando se forma o primeiro harmônico, o comprimento da corda corresponde a meio comprimento de onda:
A velocidade de propagação de uma onda é dada pela lei de Taylor:
em que F corresponde à força de tração aplicada sobre a corda e μ corresponde à densidade linear da corda. Como a corda sustenta o corpo, mantendo-o em equilíbrio, o módulo da força de tração é igual ao peso do corpo pendurado.
Substituindo as equações 1 e 2 na equação fundamental da ondulatória, tem-se:
Assim, a frequência é dada por:
No primeiro caso, tem-se:
No segundo caso, tem-se:
Dividindo a equação 4 pela equação 3, tem-se:
(elevando-se ambos os membros da equação ao quadrado)