Um marceneiro possui um pedaço de madeira no formato de um triângulo retângulo, cujos catetos medem 12 cm e 35 cm. A partir desta peça, ele precisa extrair o maior quadrado possível, de tal forma que um dos ângulos retos do quadrado coincida com o ângulo reto do triângulo. A medida do lado do quadrado desejado pelo marceneiro está mais próxima de
Do enunciado, tem-se o seguinte esboço:
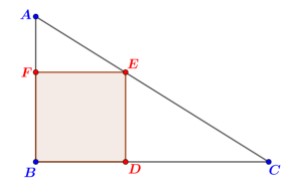
Onde AB = 12 cm, BC = 35 cm e o quadrado BDEF tem lado de medida ℓ cm.
Como ΔAFE~ΔABC tem-se