Anglo Resolve

Questão 10

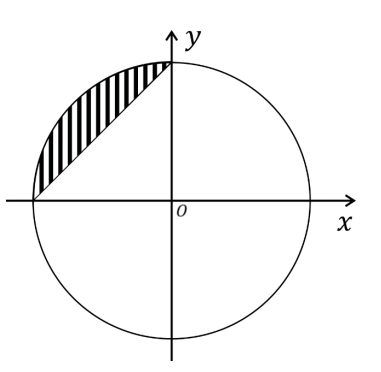
A região hachurada do plano cartesiano xOy contida no círculo de centro na origem O e raio 1, mostrada na figura, pode ser descrita por

a
{(x,y); x² + y² ≤1 e y - x ≤ 1}.
b
{(x,y); x² + y² ≥ 1 e y + x ≥ 1}.
c
{(x, y); x² + y² ≤ 1 e y - x ≥ 1}.
d
{(x,y); x² + y²≤ 1 e y + x ≥ 1}.
e
{(x,y); x² + y² ≥ 1 e y + x ≤ 1}.

Resolução

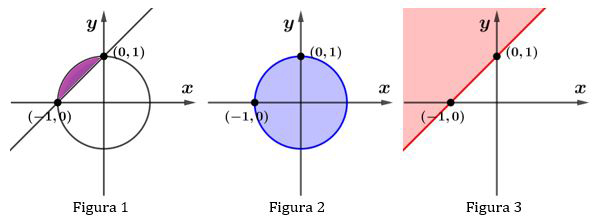
A região representada na figura 1 pode ser obtida pela intersecção das regiões representadas nas figuras 2 e 3.

A circunferência de centro (0, 0) e raio unitário é dada pela equação .
O círculo de centro (0, 0) e raio unitário é dado pela inequação (figura 2).
A reta determinada pelos pontos (–1, 0) e (0, 1) é dada pela equação , isto é, .
O semi plano determinado pela reta ao qual a origem não pertence é dado pela inequação (figura 3).

Logo, a figura 1 tem como expressão algébrica a intersecção das representações algébricas das figuras 2 e 3, isto é