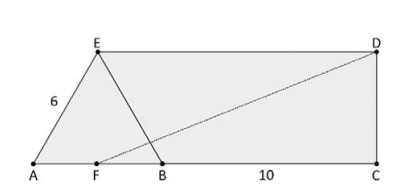
Na figura, os segmentos AC e DE são paralelos entre si e perpendiculares ao segmento CD; o ponto B pertence ao segmento AC; F é o ponto médio do segmento AB e ABE é um triângulo equilátero. Além disso, o segmento BC mede 10 unidades de comprimento e o segmento AE mede 6 unidades de comprimento. A medida do segmento DF, em unidades de comprimento, é igual a
Como ABE é um triângulo equilátero cujo lado mede 6 e F é ponto médio de , então AF = FB = 3 e
é altura relativa ao lado
, conforme indica a figura a seguir:
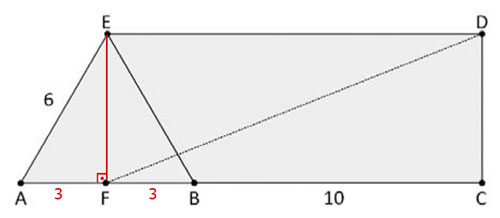
Aplicando o teorema de Pitágoras ao triângulo retângulo AFE, vem:
Além disso, no retângulo CDEF, tem-se . Assim, aplicando o teorema de Pitágoras ao triângulo retângulo CDF, obtém-se: