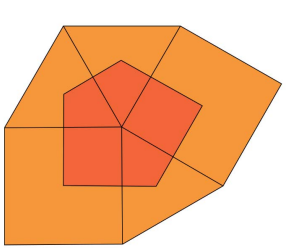
Três triângulos equiláteros e dois quadrados formam uma figura plana, como ilustrado. Seus centros são os vértices de um pentágono irregular, que está destacado na figura Se T é a área de cada um dos triângulos e Q a área de cada um dos quadrados, a área desse pentágono é
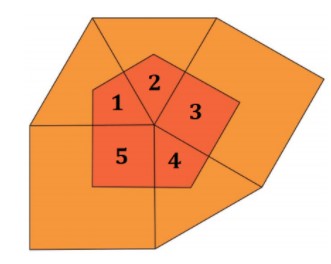
A área do pentágono irregular destacado fica dividida em 5 partes pelos lados dos triângulos e quadrados que formam a figura plana exibida. Por conta da simetria presente no triângulo equilátero, as partes 1, 2 e 4 representam, cada uma delas, um terço da área do triângulo; analogamente, as partes 3 e 5 representam, cada uma, um quarto da área do quadrado.
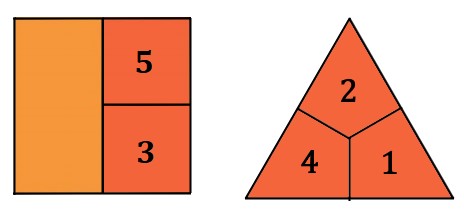
Assim, a área do pentágono é dada por: