Considere que as medidas dos lados de um triângulo retângulo estão em progressão geométrica. Sendo a a medida do menor lado e A a área desse triângulo, é correto afirmar que
Se o triângulo retângulo tem lados em progressão geométrica e o menor lado tem medida a, admitindo que a razão dessa sequência é q, com q > 1, há a seguinte representação:
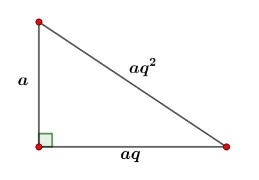
Pelo teorema de Pitágoras, tem-se
Dessa equação e como q2 > 0, tem-se
Como q > 1, tem-se
Sendo assim, a área S desse triângulo pode ser obtida por