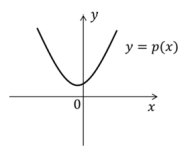
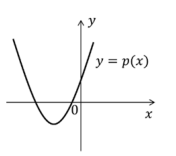
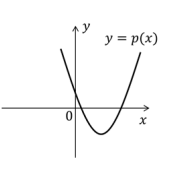
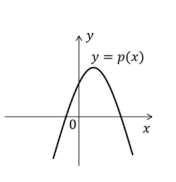
Sejam a, b, c termos consecutivos de uma progressão geométrica sem nenhum termo nulo e p(x) o polinômio de grau 2 dado por p(x) = a + bx + cx2 Se a é positivo, qual das figuras abaixo pode representar corretamente o gráfico de p (x) ?

  • a

     

  • b

  • c

  • d

Se (a, b, c) é uma P.G., denotando a razão dessa progressão por q, pode-se escrever começar estilo tamanho matemático 14px reto b espaço igual a espaço reto a vezes reto q fim do estilo e começar estilo tamanho matemático 14px reto c espaço igual a espaço reto a vezes reto q ao quadrado fim do estilo. Assim:

começar estilo tamanho matemático 14px reto p parêntese esquerdo reto x parêntese direito espaço igual a espaço reto a espaço mais espaço bx espaço mais espaço cx ao quadrado espaço igual a espaço reto a espaço mais espaço aqx espaço mais espaço aq ao quadrado reto x ao quadrado fim do estilo

 

Para obter os pontos em que a parábola intersecta o eixo das abscissas, pode-se fazer começar estilo tamanho matemático 14px reto p parêntese esquerdo reto x parêntese direito espaço igual a espaço 0 fim do estilo, ou seja, começar estilo tamanho matemático 14px reto a espaço mais espaço bx espaço mais espaço cx ao quadrado espaço igual a espaço reto a espaço mais espaço aqx espaço mais espaço aq ao quadrado reto x ao quadrado espaço igual a espaço 0 fim do estilo. O discriminante vale:

começar estilo tamanho matemático 14px incremento espaço igual a espaço parêntese esquerdo aq parêntese direito ao quadrado espaço menos espaço 4 vezes reto a vezes aq ao quadrado então espaço incremento espaço igual a espaço menos 3 reto a ao quadrado reto q ao quadrado fim do estilo

 

 

Como a e q são números reais, então o discriminante é um número negativo, o que indica que essa parábola não intersecta o eixo das abscissas. A única alternativa em que isso ocorre é a alternativa A.