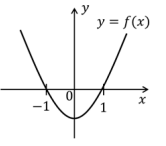
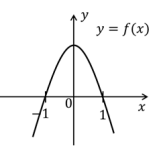
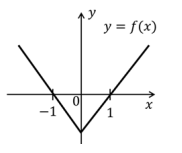
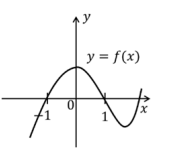
Sejam p(x) e q(x) polinômios de grau 2 tais que p(0) < q(0). Sabendo que p(1) = q(1) e p(-1) = q(-1), o gráfico de f(x) = p(x) - q(x) pode ser representado por
- Como
, então
e, portanto,
, o que elimina as alternativas B e D.
- Além disso, como
e
, se esses dois polinômios tivessem coeficientes dominantes iguais, isso faria com que
para todo x, o que é absurdo, pois
. Assim, como os coeficientes dominantes de
e
são distintos(*), então
continua sendo um polinômio do 2º grau, o que elimina a alternativa C.
Logo, dentre as alternativas apresentadas, a que melhor representa o gráfico de f é a alternativa A.
Obs: (*) Com efeito, se e
, então:
Subtraindo (II) de (I), tem-se e, portanto,
.
Substituindo em (I), tem-se e, assim,
.
Como ,
e
, tem-se
e, portanto,
, ou seja,
.
De (III) e (IV) tem-se que e, assim,
.