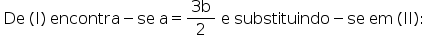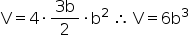A figura representa a vista superior de uma bola de futebol americano, cuja forma é um elipsoide obtido pela rotação de uma elipse em tomo do eixo das abscissas. Os valores a e b são, respectivamente, a metade do seu comprimento horizontal e a metade do seu comprimento vertical. Para essa bola, a diferença entre os comprimentos horizontal e vertical é igual à metade do comprimento vertical.
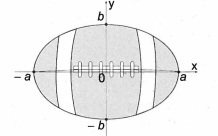
Considere que o volume aproximado dessa bola é dado por V = 4ab2.
O volume dessa bola, em função apenas de b, é dado por
Do enunciado, tem-se que 2a – 2b = b (I) e V = 4ab² (II).