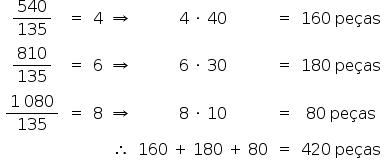Um arquiteto está reformando uma casa. De modo a contribuir com o meio ambiente, decide reaproveitar tábuas de madeira retiradas da casa. Ele dispõe de 40 tábuas de 540 cm, 30 de 810 cm e 10 de 1 080 cm, todas de mesma largura e espessura. Ele pediu a um carpinteiro que cortasse as tábuas em pedaços de mesmo comprimento, sem deixar sobras, e de modo que as novas peças ficassem com o maior tamanho possível, mas de comprimento menor que 2 m.
Atendendo o pedido do arquiteto, o carpinteiro deverá produzir
O comprimento de cada tábua deverá ser o maior divisor comum de 540, 810 e 1 080, porém menor do que 200.
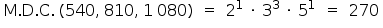
Procurando-se outros divisores comuns a partir do M.D.C., tem-se:
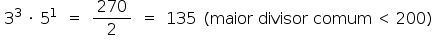
Portanto,