O acréscimo de tecnologias no sistema produtivo industrial tem por objetivo reduzir custos e aumentar a produtividade. No primeiro ano de funcionamento, uma indústria fabricou 8 000 unidades de um determinado produto. No ano seguinte, investiu em tecnologia adquirindo novas máquinas e aumentou a produção em 50%. Estima-se que esse aumento percentual se repita nos próximos anos, garantindo um crescimento anual de 50%. Considere P a quantidade anual de produtos fabricados no ano t de funcionamento da indústria.
Se a estimativa for alcançada, qual é a expressão que determina o número de unidades produzidas P em função de t, para f 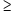 1?
1?
Para t ≥ 1:
P(t) = P0 · (1 + i)t –1
P0: produção no primeiro ano de funcionamento = 8000
i: taxa de crescimento anual: 50% = 0,5
t: anos de funcionamento, com t ≥ 1
Portanto,
P(t) = 8000 · (1,5)t –1