Uma padaria vende, em média, 100 pães especiais por dia e arrecada com essas vendas, em média, R$ 300,00. Constatou-se que a quantidade de pães especiais vendidos diariamente aumenta, caso o preço seja reduzido, de acordo com a equação
q = 400 - 100p,
na qual q representa a quantidade de pães especiais vendidos diariamente e p, o seu preço em reais.
A fim de aumentar o fluxo de clientes, o gerente da padaria decidiu fazer uma promoção. Para tanto, modificará o preço do pão especial de modo que a quantidade a ser vendida diariamente seja a maior possível, sem diminuir a média de arrecadação diária na venda desse produto.
O preço p, em reais, do pão especial nessa promoção deverá estar no intervalo
- a
R$ 0,50
p < R$ 1,50 - b
R$ 1,50
p< R$2,50 - c
R$ 2,50
p < R$ 3,50 - d
R$ 3,50 < p < R$ 4,50
- e
R$ 4,50
p < R$ 5,50
A arrecadação média é dada por p · q, onde p é o preço unitário e q é a quantidade vendida.
Do enunciado, tem-se que p · q = 300, com q = 400 – 100 · p.
Assim, tem-se que (400 – 100 · p) · p = 300 e, portanto, p2 – 4p + 3 = 0.
Resolvendo a equação, tem-se que p = 1 ou p = 3. Para p = 1, tem-se que q = 300 e, para p = 3, tem-se que q = 100. Logo, o maior valor possível de q ocorre para p = 1, ou seja, 0,50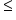 
p 
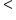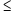1,50.