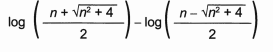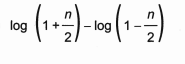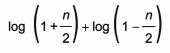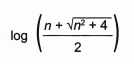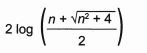Um engenheiro projetou um automóvel cujos vidros das portas dianteiras foram desenhados de forma que suas bordas superiores fossem representadas pela curva de equação y = log (x), conforme a figura.
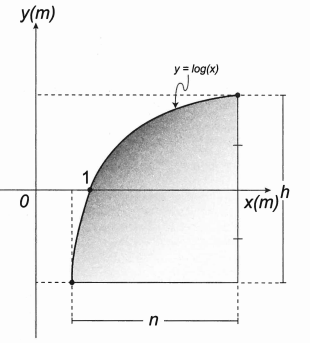
A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do vidro e a base do vidro seja paralela ao eixo x. Obedecendo a essas condições, o engenheiro determinou uma expressão que fornece a altura h do vidro em função da medida n de sua base, em metros.
A expressão algébrica que determina a altura do vidro é
Considere o ponto A (a, log a) e o ponto B (a + n, log (a + n)).
De acordo com o gráfico, sabe-se que 0<a<1.
Pelo enunciado, |log (a + n)|=|log a|.
Como log a < 0 (pelo gráfico), então:
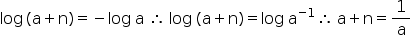
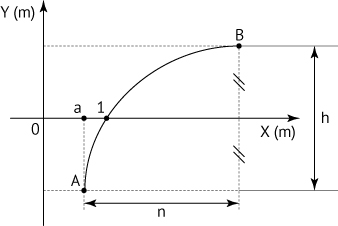
Como 0 < a < 1, tem-se:
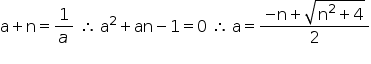
Nessas condições, a altura h será dada por 2 · log(a + n).