O índice pluviométrico é utilizado para mensurar a precipitação da água da chuva, em milímetros, em determinado período de tempo. Seu cálculo é feito de acordo com o nível de água da chuva acumulada em 1 m2, ou seja, se o índice for de 10 mm, significa que a altura do nível de água acumulada em um tanque aberto, em formato de um cubo com 1 m2 de área de base, é de 10 mm. Em uma região, após um forte temporal, verificou-se que a quantidade de chuva acumulada em uma lata de formato cilíndrico, com raio 300 mm e altura 1 200 mm, era de um terço da sua capacidade.
Utilize 3,0 como aproximação para π.
O índice pluviométrico da região, durante o período do temporal, em milímetros, é de
Como a quantidade de chuva acumulada na lata cilíndrica era de um terço de sua capacidade, então o índice pluviométrico (IP) é igual a um terço da altura da lata:

Em uma região em que a chuva é distribuída uniformemente, sem ventos muito fortes, recipientes com paredes verticais de tamanhos e bases diversas recebem a mesma quantidade de chuva por m2:
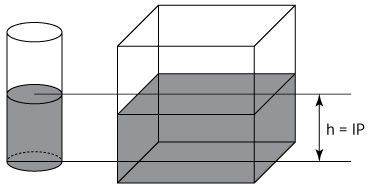
Comentário: O candidato pode ter sido levado a calcular, erroneamente, a altura que teria o mesmo volume de água da lata se fosse colocado em um cubo de 1 m2 de base:
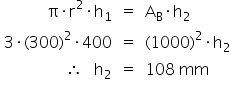
Lamentamos a falta de clareza do enunciado e a ausência de alternativa correta.
Gabarito Anglo: sem resposta
Gabarito oficial: D