• B

    .

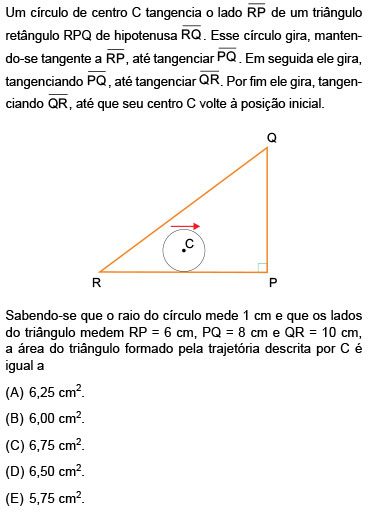
A figura a seguir retrata os instantes em que o centro do círculo determina cada um dos vértices do triângulo ABC formado, assim como os pontos de tangência do círculo com os lados do triângulo original:

Como os triângulos PQR e ABC são semelhantes, tem-se:

começar estilo tamanho matemático 14px AB sobre PQ espaço igual a espaço BC sobre QR espaço igual a espaço AC sobre PR espaço igual a espaço reto k espaço espaço espaço então AB espaço igual a espaço 8 reto k espaço espaço espaço espaço espaço vírgula espaço espaço espaço espaço espaço BC espaço igual a espaço 10 reto k espaço espaço espaço espaço espaço reto e espaço espaço espaço espaço espaço AC espaço igual a espaço 6 reto k fim do estilo

Além disso, como começar estilo tamanho matemático 14px AC espaço igual a espaço reto A com 1 subscrito reto C com 2 subscrito fim do estilo, tem-se que começar estilo tamanho matemático 14px RC com 2 subscrito espaço igual a espaço PR espaço menos espaço 1 espaço menos espaço reto A com 1 subscrito reto C com 2 subscrito espaço igual a espaço 5 espaço menos espaço 6 reto k fim do estilo. 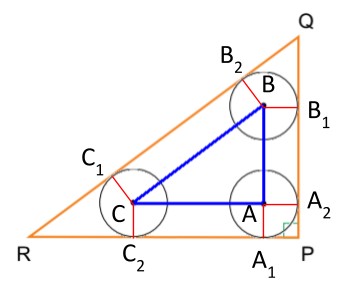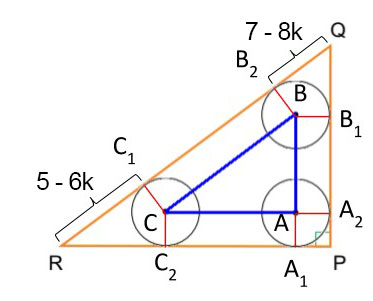Aplicando raciocínio análogo, pode-se concluir que começar estilo tamanho matemático 14px QB com 1 subscrito espaço igual a espaço PQ espaço menos espaço 1 espaço menos espaço reto A com 2 subscrito reto B com 1 subscrito espaço igual a espaço 7 espaço menos espaço 8 reto k fim do estilo.

Pela tangência, tem-se que começar estilo tamanho matemático 14px QB com 1 subscrito espaço igual a espaço QB com 2 subscrito fim do estilo e começar estilo tamanho matemático 14px RC com 1 subscrito espaço igual a espaço RC com 2 subscrito fim do estilo. Veja a figura seguir:

 

Por fim, como começar estilo tamanho matemático 14px reto B com 2 subscrito reto C com 1 subscrito espaço igual a espaço BC fim do estilo, tem-se:

começar estilo tamanho matemático 14px atributos de tabela alinhamento de coluna right center left espaçamento de coluna 0px fim dos atributos linha com célula com QR espaço fim da célula igual a célula com espaço 5 espaço menos espaço 6 reto k espaço mais espaço BC espaço mais 7 espaço menos espaço 8 reto k espaço espaço espaço então fim da célula linha com célula com 10 espaço fim da célula igual a célula com espaço 5 espaço menos espaço 6 reto k espaço mais espaço estreito 10 reto k espaço mais espaço 7 espaço menos espaço 8 reto K espaço espaço espaço então fim da célula linha com célula com reto k espaço fim da célula igual a célula com espaço 1 meio fim da célula fim da tabela fim do estilo

Dessa forma, os catetos do triângulo ABC medem começar estilo tamanho matemático 14px 6 reto k espaço igual a espaço 3 fim do estilo e começar estilo tamanho matemático 14px 8 reto k espaço igual a espaço 4 fim do estilo, sendo sua área, portanto, igual a:

começar estilo tamanho matemático 14px numerador 3 vezes 4 sobre denominador 2 fim da fração espaço igual a espaço 6 fim do estilo