Um garoto foi à loja comprar um estilingue e encontrou dois modelos: um com borracha mais “dura” e outro com borracha mais “mole”. O garoto concluiu que o mais adequado seria o que proporcionasse maior alcance horizontal, D, para as mesmas condições de arremesso, quando submetidos à mesma força aplicada. Sabe-se que a constante elástica kd (do estilingue mais “duro”) é o dobro da constante elástica km (do estilingue mais “mole”).
A razão entre os alcances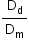 
, referentes aos estilingues com borrachas “dura” e “mole”, respectivamente, é igual a
- a
. - b
. - c
1.
- d
2.
- e
4.
As figuras a seguir representam todo o processo, descrito de maneira esquemática.
- Figura 1: elástico na posição de deformação máxima.
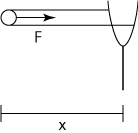
- Figura 2: elástico sem deformação e corpo abandonando o elástico.
- Figura 3: descrição de todo o lançamento, que será considerado oblíquo e a partir do solo:
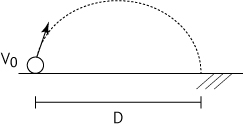
De acordo com o enunciado, os dois elásticos foram submetidos a forças de mesma intensidade:
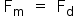
Admitindo-se que ambos os elásticos deformem no regime elástico de deformação:
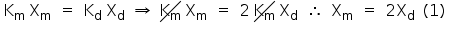
Enquanto o elástico volta ao seu comprimento natural (entre figuras 1 e 2), a única força aplicada no corpo é a elástica. Assim, entre as figuras 1 e 2, o sistema é conservativo.
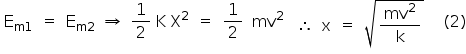
A expressão (2) vale para ambas as situações (com mola dura e mole). Portanto, utilizando-se a expressão (1):
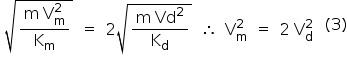
O alcance horizontal é dado por:
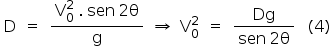
Aplicando-se a expressão (3) em (4):
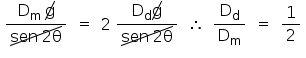
Obs.: Caso não seja feita a hipótese do lançamento oblíquo a partir do solo, não há alternativa que satisfaça as informações dadas no enunciado.
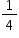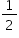