Ligando as representações dos afixos de quatro números complexos no plano de ArgandGauss obtém-se o quadrado destacado em cinza, indicado na figura por Q.
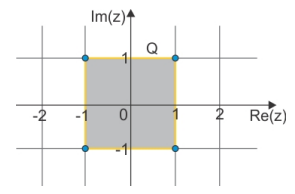
Multiplicando-se esses afixos pelo número complexo 1 + i, o polígono que será obtido, ligandose os quatro novos afixos, será um quadrado q. Comparando-se a transformação de Q em q, pode-se afirmar que houve
- a
uma reflexão pelo eixo Im(z) e outra pelo eixo Re(z).
- b
uma translação horizontal e uma vertical, ambas de uma unidade.
- c
uma rotação de 45° e os comprimentos dos lados foram multiplicados por 4.
- d
uma rotação de 90° e os comprimentos dos lados foram multiplicados por 2.
- e
uma rotação de 45° e os comprimentos dos lados foram multiplicados por
.
Do enunciado, tem-se:
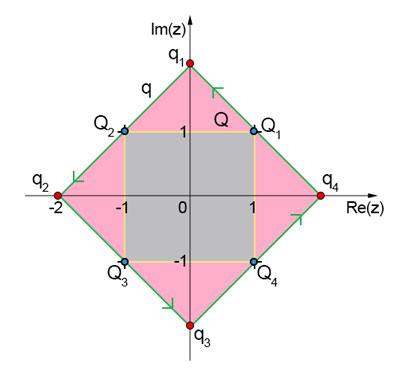
Multiplicando os quatro números complexos por 1 + i, vem:
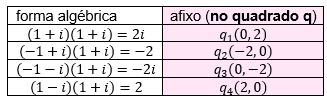
Note que:
- houve uma rotação de
no sentido anti-horário.
- os lados de Q têm medida
e os lados de q têm medida
.
Portanto, na transformação de Q em q, houve uma rotação de e os comprimentos dos lados foram multiplicados por
.