A figura mostra dois recipientes cilíndricos idênticos, R e S, de altura 35 cm, contendo água até diferentes alturas, hR e hS.
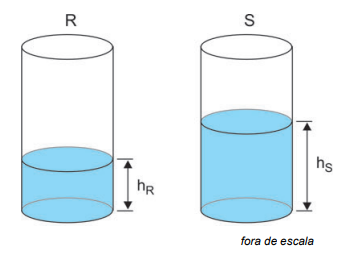
Colocando-se um alto-falante que emite um som de frequência 850 Hz sobre cada recipiente, separadamente, verifica-se que eles funcionam como tubos sonoros fechados em uma extremidade e abertos na outra, ocorrendo ressonância em ambos. Considerando-se a velocidade de propagação do som no ar igual a 340 m/s, a diferença entre as alturas da água nos dois recipientes, hS – hR, é igual a
A partir dos dados fornecidos para a velocidade do som no ar e para a frequência da onda sonora, é possível determinar o comprimento de onda:
Dentro dos tubos formam-se ondas estacionárias de modo que na extremidade aberta observa-se a formação de um ventre e na extremidade fechada observa-se um nó. Embora não seja possível determinar a ordem do modo de vibração em cada situação, a distância entre as superfícies dos líquidos deve corresponder a meio comprimento de onda, sendo N = 0, 1, 2, ...
Para N = 0:
Para N = 1:
Para N = 2:
A partir dos cálculos acima, é possível concluir que, à medida que N aumenta, também aumenta o valor da diferença entre as alturas. Dessa forma, a diferença entre as alturas, entre as alternativas fornecidas, é 0,2 m = 20 cm e essa situação corresponde à formação de harmônicos consecutivos nos tubos sonoros.