Um motorista, que conduz seu caminhão com velocidade constante de 25 m/s (90 km/h) por uma estrada retilínea, plana e horizontal, aciona os freios quando percebe um ônibus a sua frente deslocando-se lentamente no mesmo sentido, com velocidade constante de 5 m/s (18 km/h). Supondo-se que a distância entre o caminhão e o ônibus no instante em que o motorista do caminhão aciona os freios é de 80 m, que o ônibus não altera sua velocidade e que não há mudança nas direções dos movimentos de ambos os veículos, o módulo da aceleração mínima, admitida constante, que deve ser imprimida ao caminhão para evitar a colisão é

  • a

    1,5 m/s2.

  • b

    2,5 m/s2.

  • c

    3,0 m/s2.

  • d

    3,5 m/s2.

  • e

    4,0 m/s2.

A situação descrita no enunciado pode ser representada da seguinte maneira:

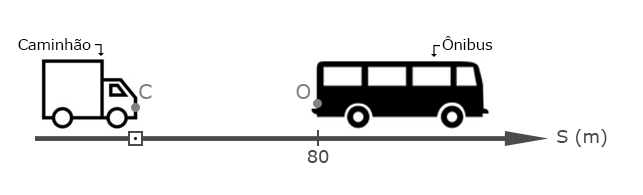
De acordo com o enunciado:

  • A aceleração do caminhão C é constante, logo, ele executa um movimento uniformemente retardado;
  • O ônibus desenvolve velocidade constante, logo, executa movimento uniforme;

Dessa forma, podemos assim representar suas funções horárias dos espaços:

começar estilo tamanho matemático 14px reto s com reto C subscrito espaço igual a espaço reto s com 0 reto C subscrito fim do subscrito espaço mais espaço reto v com 0 reto C subscrito fim do subscrito reto t espaço mais espaço at ao quadrado sobre 2 espaço seta para a direita espaço reto s com reto C subscrito espaço igual a espaço 0 mais 25 reto t espaço mais espaço at ao quadrado sobre 2 fim do estilo (equação 1)
começar estilo tamanho matemático 14px reto s com reto O subscrito espaço igual a espaço reto s com 0 reto O subscrito fim do subscrito espaço mais espaço vt espaço seta para a direita espaço reto s com reto O subscrito espaço igual a espaço 80 espaço mais espaço 5 reto t fim do estilo (equação 2)

A fim de evitar a colisão, para que a aceleração seja mínima, podemos impor que:

  1. A mínima aceleração constante do caminhão é obtida quando sua velocidade final é igual à velocidade do ônibus:
    começar estilo tamanho matemático 14px reto v com reto C subscrito espaço igual a espaço reto v com 0 reto C subscrito fim do subscrito espaço mais espaço reto a espaço vezes espaço reto t espaço seta para a direita espaço 5 espaço igual a espaço 25 espaço mais espaço reto a espaço vezes espaço reto t espaço então espaço reto a espaço vezes espaço reto t espaço igual a espaço menos 20 fim do estilo (equação 3)

  2. A posição do para-choque dianteiro do caminhão deve estar na mesma posição que o para-choque traseiro do ônibus. Para isso, igualamos as equações 1 e 2:
    começar estilo tamanho matemático 14px reto s com reto C subscrito espaço igual a espaço reto s com reto O subscrito espaço seta para a direita espaço 0 espaço mais espaço 25 reto t espaço mais espaço at ao quadrado sobre 2 espaço igual a espaço 80 espaço mais espaço 5 reto t espaço seta para a direita espaço 20 reto t espaço mais espaço at ao quadrado sobre 2 espaço igual a espaço 80 espaço fim do estilo

Substituindo a equação 3 na expressão anterior, tem-se:

começar estilo tamanho matemático 14px 20 reto t espaço mais espaço at ao quadrado sobre 2 espaço igual a espaço 80 espaço seta para a direita espaço 20 reto t espaço mais espaço at reto t sobre 2 espaço igual a espaço 80 espaço seta para a direita espaço 20 reto t espaço menos espaço 10 reto t espaço igual a espaço 80 espaço espaço então espaço reto t espaço igual a espaço 8 espaço reto s fim do estilo

Substituindo esse valor na equação 3, tem-se:

começar estilo tamanho matemático 14px at espaço igual a espaço menos 20 espaço seta para a direita espaço reto a 8 espaço igual a espaço menos 20 espaço seta para a direita espaço reto a espaço igual a espaço menos 2 vírgula 5 espaço reto m sobre reto s ao quadrado espaço então espaço abre barra vertical reto a fecha barra vertical espaço igual a espaço 2 vírgula 5 espaço reto m sobre reto s ao quadrado fim do estilo