A figura indica um cone circular reto de vértice V e centro da base C. O quadrilátero PQRS é um quadrado de área igual a 8 cm² cujo plano suporte determina com a base do cone um diedro de 45°.
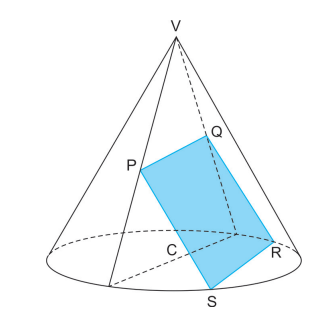
A área da base desse cone é igual a
A partir da figura do enunciado, considerando-se a figura a seguir:
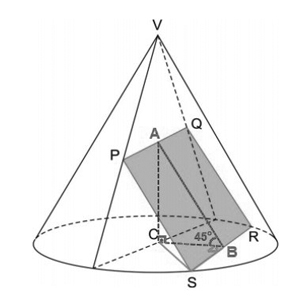
No triângulo retângulo ABC, tem-se que a medida AB da hipotenusa vale =
cm. Além disso, note-se que:
No triângulo retângulo CBS, tem-se . Aplicando o teorema de Pitágoras a esse triângulo, tem que:
Como CS é a medida do raio da base do cone, conclui-se que a área da base desse cone vale π ∙ (CS)2 = 6π cm2.
Resposta: 6π cm2