O esquema a seguir indica o algoritmo da multiplicação aplicado à multiplicação de um número inteiro de três algarismos por outro de quatro algarismos, resultando em um número inteiro de seis algarismos.
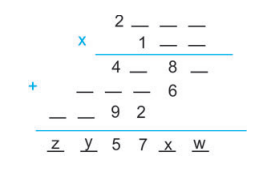
O valor de x – w + z – y é
Observando a figura a seguir, em que cada uma das linhas do procedimento foi numerada.
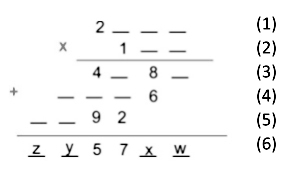
A linha (5) exibe o resultado da multiplicação entre 1 e o número da linha (1), ou seja, a linha (5) e a linha (1) exibem o mesmo número.
Assim, pode-se reescrever:
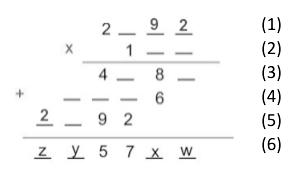
Como a linha (3) exibe o resultado da multiplicação entre o algarismo das unidades do número da linha (2) e o número da linha (1), tem-se que o algarismo das unidades do número da linha (1) é 2. Assim, o algarismo das unidades do número da linha (3) é 4 e, reescrevendo, chega-se a:
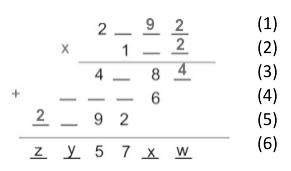
Como a linha (4) exibe o resultado da multiplicação entre o algarismo das dezenas do número da linha (2) e o número da linha (1), tem-se que o algarismo das dezenas do número da linha (1) é 3. Dessa forma, pode-se concluir que o algarismo das dezenas do número da linha (4) é 7. Reescrevendo, tem-se:
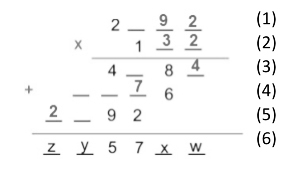
Dessa forma, pode-se concluir que:
- w = 4
- x é o algarismo das unidades da soma 8 + 6, ou seja, x = 4
- como a soma 8 + 6 resultou em um número maior que 9, tem-se que o algarismo 7 do número exibido na linha (6) é o algarismo das unidades da soma entre 1 (dezena da soma 8 + 6), 7, 2 e o algarismo das centenas do número exibido na linha (4). Assim, esse algarismo é igual a 7.
- como o algarismo das centenas do número exibido na linha (3) é 7, tem-se que o algarismo das centenas do número exibido na linha (1) é 3.
Assim, o esquema ilustra a multiplicação entre os números 132 e 2392, que resulta em 315744, de modo que z = 3 e y = 1. Tem-se, portanto, que
x – w + z – y = 4 – 4 + 3 – 1 = 2
Resposta: 2