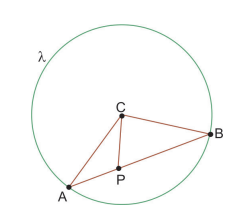
A figura representa um círculo λ de centro C. Os pontos A e B pertencem à circunferência de λ e o ponto P pertence a . Sabe-se que PC = PA = k e que PB = 5, em unidades de comprimento.
A área de λ, em unidades de área, é igual a
Denotando a medida do ângulo por ∝, tem-se que:
- a medida do ângulo
é ∝, já que o triângulo APC é isósceles;
- a medida do ângulo
é ∝, já que o triângulo ABC é isósceles.
Denotando por R a medida do raio da circunferência λ, a figura a seguir ilustra o que foi escrito.
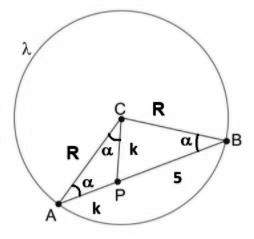
Dessa forma, os triângulos APC e BCA são semelhantes. Assim, tem-se:
Como a área do círculo dado λ por é πR2, tem-se que essa área é igual a: