As coordenadas cartesianas dos vértices da base do triângulo isósceles FGV são F(6, 0) e G(0, 6). Sendo m e n os dois valores possíveis de abscissa de V para que a área de FGV seja igual a 6 unidades de área do plano cartesiano, o valor de m + n é
Do enunciado, tem-se a figura a seguir.
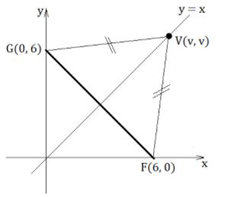
O ponto V pertence à reta de equação y = x.
Pode-se representar V por (v, v).
Sendo D = , tem-se D = 36 – 12v = 12 (3 – v).
A área do triângulo é dada por
Sendo essa área igual a 6, tem-se:
ou
v = 2 ou v = 4
Os valores de m e n são 2 e 4 (não necessariamente nessa ordem).
Logo, m + n = 6.
Resposta: 6