As retas r e s são secantes à circunferência λ, de equação (x – 3)2 + (y – 1)2 = 13, nos pontos P, Q e T, sendo que em P elas se intersectam formando um ângulo de 30°, como mostra a figura.
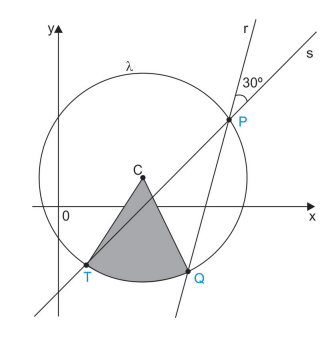
Sendo C o centro de λ, a área do setor circular destacado em cinza na figura, em unidades de área do sistema cartesiano de eixos ortogonais, é igual a
Na figura, note-se que as retas r e s determinam em λ o ângulo inscrito correspondente ao ângulo central
. Como
, tem-se que
.
Como a medida do raio de λ é unidades de comprimento, a área A do setor circular destacado em cinza, em unidades de área, é:
Resposta:
Alternativa D