Os lados do paralelogramo FGVE medem 5 e 8 centímetros. As mediatrizes de indicadas por m e n, intersectam-se no ponto C, que é centro da circunferência λ, de raio CE = CF, como mostra a figura.
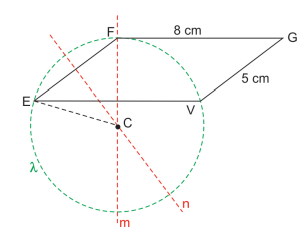
Sabendo que a mediatriz m passa pelo vértice F, a área do triângulo FEC é igual a
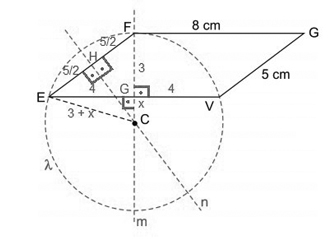
A partir das mediatrizes de e
, tem-se que:
e
.
Note-se que o triângulo EFG é pitagórico, com FG = 3 cm.
Além disso, CF = CE = raio, logo o triângulo EFC é isósceles de base 5.
Chamando CG = x, tem-se que EC = 3 + x, e, aplicando Pitágoras no triângulo EGC, tem-se: .
Assim, .
No triângulo CHF, por Pitágoras, tem-se:
Assim, a área do triângulo FEC será:
.
Resposta:
Alternativa E