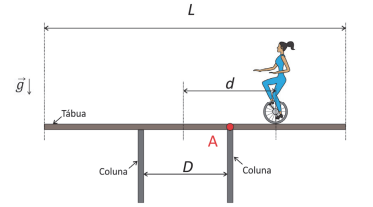
Uma equilibrista de massa M desloca‐se sobre uma tábua uniforme de comprimento L e massa m apoiada (sem fixação) sobre duas colunas separadas por uma distância D (D<L) de modo que o centro da tábua esteja equidistante das colunas. O ponto de apoio da equilibrista está a uma distância d (tal que D/2 <d<L/2) do centro da tábua, como mostra a figura.
a) Considerando que a tábua está em equilíbrio, faça um diagrama indicando todas as forças que atuam sobre a tábua e seus respectivos pontos de aplicação.
b) Calcule o torque resultante exercido pelos pesos da equilibrista e da tábua em relação ao ponto A (ponto de apoio da tábua na coluna mais próxima da equilibrista). Escreva sua resposta em termos de grandezas mencionadas no enunciado (M, L, m, D, d) e da aceleração da gravidade g.
c) Calcule a distância máxima dmáx da equilibrista ao centro da tábua para que o conjunto permaneça em equilíbrio estático. Considere os seguintes dados: comprimento da tábua: L = 5 m; massa da tábua: m = 20 kg, massa da equilibrista: M = 60 kg, distância entre as colunas: D = 3 m.
Note e adote:
Despreze as espessuras da tábua e da coluna.
Use g = 10 m/s2
a) O diagrama seguinte indica todas as forças que atuam sobre a tábua:

Em que:
e
são as forças aplicadas pelos apoios A e B na tábua.
é o peso aplicado na tábua, aplicado no ponto médio de
.
é a normal que a equilibrista aplica na tábua, no ponto de contato com o pneu. Ela tem mesma intensidade que o peso aplicado na equilibrista.
b) O torque resultante do peso aplicado na equilibrista e do peso aplicado na tábua
em relação ao ponto A é:
c) Quando a equilibrista estiver posicionada à maior distância (dmax) do centro da tábua, a normal do apoio B será nula (iminência de tombamento). Logo:
Substituindo-se os dados do enunciado: