Resolva os três itens abaixo:
a) Considere o conjunto formado pelos números complexos ݖ que cumprem a condição Re(z) = Im(z). Cada elemento desse conjunto será objeto da transformação que leva um número complexo em seu conjugado. Represente no plano complexo (ou plano de Argand‐Gauss) da folha de respostas o conjunto resultante após essa transformação.
b) Determine o lugar geométrico dos pontos z do plano complexo tais que z ≠ -1 e para os quais é um número imaginário puro.
c) Determine as partes reais de todos os números complexos z tais que as representações de z, i e 1 no plano complexo sejam vértices de um triângulo equilátero.
Considere z = x + yi, com x e y reais.
a) De Re(z) = Im(z) vem: y = x.
Fazendo-se a transformação pedida, a cada é associado
, ou seja
.
Os pontos que representam esse conjunto no plano de Argand-Gauss são da forma (x, –x) e estão sobre a reta suporte das bissetrizes dos quadrantes pares.
Resposta:
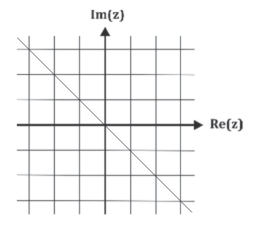
b)
Para que seja imaginário puro, deve-se ter:
De (1) e (2) vem e
O lugar geométrico é uma circunferência com centro na origem e raio 1, menos os pontos (–1; 0) e (1; 0).
Resposta: Circunferência com centro na origem e raio 1, menos os pontos (–1; 0) e (1; 0).
c) As representações de ,
e
no plano complexo são, respectivamente (x; y), (0; 1) e (1; 0)
Como esses pontos são vértices de um triângulo equilátero, tem-se:
Dessas igualdades tem-se:
De (1) vem
Substituindo-se em (2), tem-se:
As partes reais dos números pedidos são e
.
Resposta: e
.