São dados:

• uma circunferência ܵS de centro ܱO e raio 5;

• quatro pontos ܺX, Y, Z e W em ܵS de tal forma que as retas tangentes a ܵS nesses pontos formam um trapézio ABCD, como na figura;

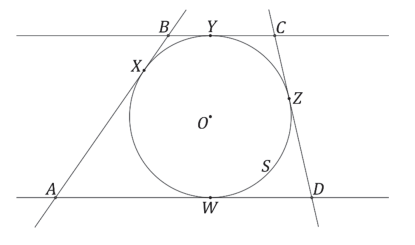
• começar estilo tamanho matemático 14px sen espaço abre parênteses pilha B A W com conjunção lógica acima fecha parênteses igual a 3 sobre 5 espaço e espaço C D igual a 15. fim do estilo

Determine
a) a medida de começar estilo tamanho matemático 14px A B em moldura superior fecha moldura fim do estilo;
b) a medida de começar estilo tamanho matemático 14px A W em moldura superior fecha moldura espaço reto e espaço A X em moldura superior fecha moldura fim do estilo;ܺ
c) a área da região delimitada pelo trapézio ABCD.

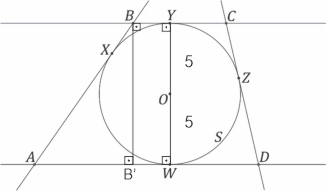
a) Do enunciado, tem-se a figura a seguir, em que a altura do trapézio ABCD é o diâmetro da circunferência, ou seja, começar estilo tamanho matemático 14px YW espaço igual a espaço BB apóstrofo espaço igual a espaço 10 fim do estilo



No triângulo retângulo ABB' tem -se:

começar estilo tamanho matemático 14px numerador espaço BB apóstrofo sobre denominador AB fim da fração espaço igual a espaço sem espaço parêntese esquerdo BÂW parêntese direito fim do estilo começar estilo tamanho matemático 14px então espaço 10 sobre AB espaço igual a espaço 3 sobre 5 espaço espaço espaço então espaço espaço AB espaço igual a espaço 50 sobre 3 fim do estilo
começar estilo tamanho matemático 14px Resp espaço então espaço 50 sobre 3 fim do estilo

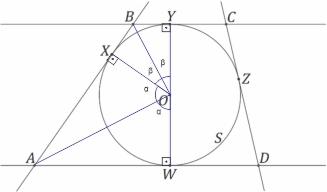
b) Considerando-se a figura a seguir, em que começar estilo tamanho matemático 14px incremento BOX espaço idêntico espaço incremento BOY espaço fim do estiloe começar estilo tamanho matemático 14px incremento AOX espaço idêntico espaço incremento AOW fim do estilo



Então, começar estilo tamanho matemático 14px 2 reto alfa espaço mais espaço 2 reto beta espaço igual a espaço 180 sinal de grau espaço então espaço reto alfa espaço mais espaço reto beta espaço igual a espaço 90 sinal de grau fim do estilo, logo, o triângulo AOB é retângulo em O.
Das relações métricas no triângulo retângulo, tem-se que começar estilo tamanho matemático 14px AX espaço vezes espaço BX espaço igual a espaço OX ao quadrado fim do estilo. Sendo começar estilo tamanho matemático 14px AX espaço igual a espaço reto x fim do estilo, com começar estilo tamanho matemático 14px AX espaço maior que espaço BX fim do estilo, vem:
começar estilo tamanho matemático 14px reto x espaço vezes espaço abre parênteses 50 sobre 3 espaço menos espaço reto x fecha parênteses espaço igual a espaço 5 ao quadrado fim do estilo
começar estilo tamanho matemático 14px 3 reto x ao quadrado espaço menos espaço 50 reto x espaço mais espaço 75 espaço igual a espaço 0 fim do estilo
começar estilo tamanho matemático 14px reto x espaço igual a espaço 15 espaço ou espaço reto x espaço igual a espaço 5 sobre 3 fim do estilo
Como começar estilo tamanho matemático 14px AX espaço maior que espaço BX vírgula espaço reto x espaço igual a espaço 15 fim do estilo

Resposta: 15

c) como o trapézio é circunscritível,
 
começar estilo tamanho matemático 14px AD espaço estreito mais espaço estreito BC espaço igual a espaço AB espaço mais espaço estreito CD AD espaço mais espaço estreito BC espaço igual a espaço 50 sobre 3 espaço mais espaço 15 AD espaço mais espaço estreito BC espaço igual a espaço 95 sobre 3 fim do estilo
A área delimitada pelo trapézio é dada por começar estilo tamanho matemático 14px reto A com reto T subscrito espaço igual a espaço numerador abre parênteses AD espaço mais espaço BC fecha parênteses espaço vezes espaço YW sobre denominador 2 fim da fração fim do estilo, logo
começar estilo tamanho matemático 14px reto A com reto T espaço subscrito fim do subscrito espaço igual a espaço numerador começar estilo mostrar 95 sobre 3 fim do estilo espaço vezes espaço 10 sobre denominador 2 fim da fração espaço espaço então espaço espaço espaço reto A com reto T subscrito espaço igual a espaço 475 sobre 3 fim do estilo
Respostas: começar estilo tamanho matemático 14px 475 sobre 3 fim do estilo