Um jogo educativo possui 16 peças nos formatos: círculo, triângulo, quadrado e estrela, e cada formato é apresentado em 4 cores: amarelo, branco, laranja e verde. Dois jogadores distribuem entre si quantidades iguais dessas peças, de forma aleatória. O conjunto de 8 peças que cada jogador recebe é chamado de coleção.
a) Quantas são as possíveis coleções que um jogador pode receber?
b) Qual é a probabilidade de que os dois jogadores recebam a mesma quantidade de peças amarelas?
c) A regra do jogo estabelece pontuações para as peças, da seguinte forma: círculo = 1 ponto, triângulo = 2 pontos, quadrado = 3 pontos e estrela = 4 pontos. Quantas são as possíveis coleções que valem 26 pontos ou mais?
a) Como a ordem na qual cada jogador recebe cada uma das 8 peças da sua coleção não importa, o número de maneiras de isso ocorrer é dado por
Resposta: 12 870.
b) Para que os dois jogadores recebam quantidades iguais de peças amarelas, cada um deve receber exatamente duas peças amarelas e seis peças de outras cores.
O número de modos de isso ocorrer é dado por .
Assim, a probabilidade p pedida é
Resposta .
c) Apresentando-se, por meio de uma tabela, as situações que geram 26 ou mais pontos.
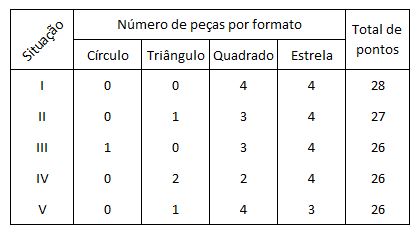
- Para a situação I, existe 1 coleção
- Para a situação II, existem
- Para a situação III, existem
- Para a situação IV, existem
- Para a situação V, existem
Portanto, o número de possíveis coleções que valem 26 ou mais pontos é
1 + 16 + 16 + 36 + 16 = 85.
Resposta: 85.