No plano cartesiano de eixos ortogonais foi desenhada uma circunferência λ, de centro A e equação geral x2 + y2 – 4x – 6y – 12 = 0. Os pontos B, C, D e E pertencem a λ, sendo um diâmetro de λ. Sabe-se ainda que a medida do ângulo C
B é de 30º e que
e
são segmentos paralelos.
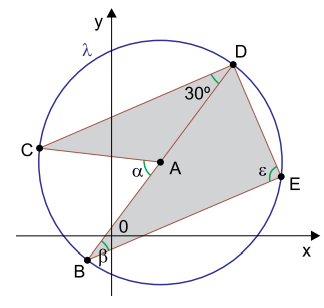
a) Determine as medidas dos ângulos indicadas na figura por α, β e ε.
b) Calcule a área do pentágono côncavo ACDEB, destacado na figura em cinza.
a)
b)
Resolução:
a) Considere-se a figura a seguir:
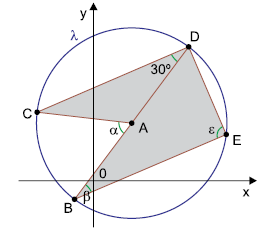
O ângulo é o ângulo central correspondente ao ângulo inscrito
, logo
.
Como e
são paralelos,
e
são alternos internos, logo
.
O ângulo está inscrito em uma semicircunferência, logo
.
b)
A circunferência tem centro A (2, 3) e raio medindo 5.
Considere-se a figura a seguir:
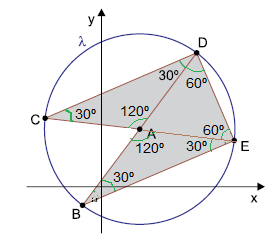
Tem-se AC = AD = AE = AB = 5.
A área A do pentágono côncavo ACDEB é igual à soma das áreas dos triângulos ACD, ADE e AEB, logo: