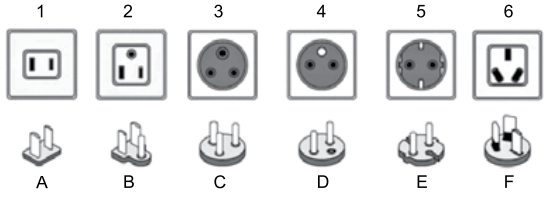
A figura indica seis tipos de tomadas e os pinos projetados para nelas se encaixarem (1-A, 2-B, 3-C, 4-D, 5-E e 6-F). Além dessa correspondência, sabe-se que:
• O pino A também se encaixa na tomada 2.
• O pino D também se encaixa nas tomadas 3 e 5.
• O pino E também se encaixa nas tomadas 3 e 4.
a) Sorteando-se aleatoriamente um tipo de pino e um tipo de tomada, qual é a probabilidade de que o encaixe entre eles possa ser feito?
b) Sorteando-se aleatoriamente dois tipos de tomadas e dois tipos de pinos, qual é a probabilidade de que seja possível conectar um deles a uma tomada e o outro a outra?
a) Para que o encaixe possa ser feito, pode-se sortear:
|
o pino (A) E uma das tomadas (1 OU 2) |
OU |
o pino (B) E a tomada (2) |
OU |
o pino (C) E a tomada (3) |
OU |
o pino (D) E uma das tomadas (3, 4 OU 5) |
OU |
o pino (E) E uma das tomadas (3, 4 OU 5) |
OU |
o pino (F) E a tomada (6) |
Assim, a probabilidade pedida é
b) Há 15 formas de se escolherem duas tomadas distintas e 15 formas de se escolherem dois tipos de pino distintos, de modo que há
formas de se escolherem duas tomadas distintas e dois tipos de pinos distintos.
Analisando-se todas as 15 formas de se escolherem duas tomadas distintas:
- A e B:
- pinos 1 e 2
Apenas 1 caso possível.
- A e C:
- pinos 1 e 2
- pinos 2 e 3
Apenas 2 casos possíveis.
- (A e D) ou (A e E):
- pinos 1 e 3
- pinos 1 e 4
- pinos 1 e 5
- pinos 2 e 3
- pinos 2 e 4
- pinos 2 e 5
Apenas 12 casos possíveis.
- A e F:
- pinos 1 e 6
- pinos 2 e 6
Apenas 2 casos possíveis.
- B e C:
- pinos 2 e 3
Apenas 1 caso possível.
- (B e D) ou (B e E):
- pinos 2 e 3
- pinos 2 e 4
- pinos 2 e 5
Apenas 6 casos possíveis.
- B e F:
- pinos 2 e 6
Apenas 1 caso possível.
- (C e D) ou (C e E):
- pinos 3 e 4
- pinos 3 e 5
Apenas 4 casos possíveis.
- C e F:
- pinos 3 e 6
Apenas 1 caso possível.
- D e E:
- pinos 3 e 4
- pinos 3 e 5
- pinos 4 e 5
Apenas 3 casos possíveis.
- (D e F) ou (E e F):
- pinos 3 e 6
- pinos 4 e 6
- pinos 5 e 6
Apenas 6 casos possíveis.
Assim, são 39 casos favoráveis, em um total de 225 casos. Dessa forma, a probabilidade pedida é:
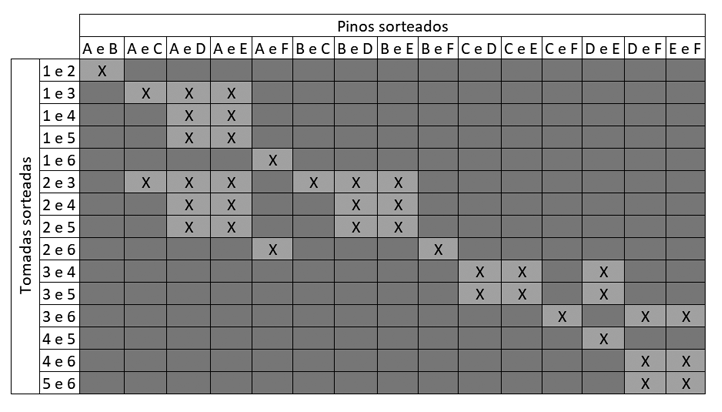
Observação: contemplando-se todos os casos em um quadro de possibilidades, denotando por “X” os encaixes possíveis, tem-se: