Para determinar a densidade de uma coroa metálica maciça, foi realizado um experimento em que ela foi pendurada em um dinamômetro ideal por dois modos diferentes: um no ar e outro totalmente imersa na água em equilíbrio contida em um recipiente, de acordo com as figuras 1 e 2, respectivamente. Na primeira situação, o dinamômetro indicou 8,0 N e, na segunda situação, indicou 7,6 N.
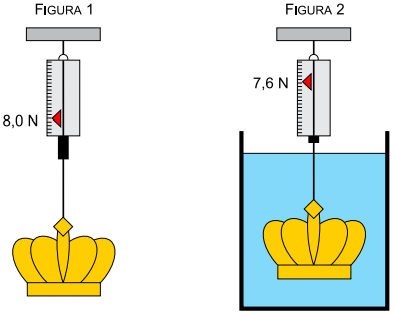
Sabendo que a densidade da água é 103 kg/m3 e adotando g = 10 m/s2,
a) represente as forças que agem na coroa na situação da figura 2 e calcule a massa dessa coroa, em kg.
b) calcule a densidade, em kg/m3, dessa coroa.
a) Na figura 2, tem-se:
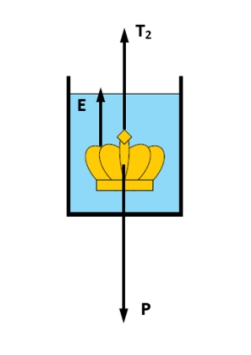
Em que:
- P: peso aplicado na coroa;
- E: empuxo aplicado pela água sobre a coroa;
- T2: tração aplicada pelo fio na situação ilustrada.
Já na figura 1, tem-se:
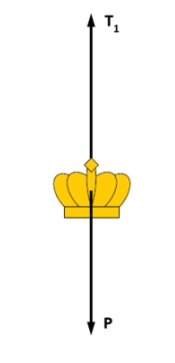
Como a coroa está em repouso e, observando-se na figura 1, T1 = 8N:
b) Na figura 2, a coroa também está em repouso. Observando-se que T2 = 7,6 N:
Como a coroa está completamente imersa, Vdeslocado = Vcoroa. Substituindo os dados fornecidos:
A partir desse resultado, pode-se calcular a densidade da coroa: