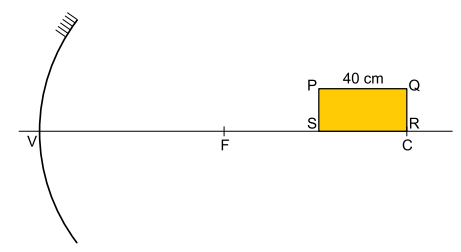
Uma placa retangular de espessura desprezível e de vértices PQRS é posicionada, em repouso, sobre o eixo principal de um espelho esférico gaussiano de vértice V, foco principal F e centro de curvatura C, de modo que a posição do vértice R da placa coincida com a posição do ponto C, conforme figura. O raio de curvatura desse espelho mede 160 cm e o comprimento da placa é 40 cm.
a) Na figura apresentada no campo de Resolução e Resposta, construa, traçando raios de luz, a imagem P’S’ do lado PS dessa placa. Identifique, nessa figura, os pontos P’ e S’ e classifique essa imagem como real ou virtual, justificando sua resposta.
b) Calcule, em cm, a distância entre a imagem P’S’, do lado PS, e a imagem Q’R’, do lado QR.
a) A imagem é real e invertida.
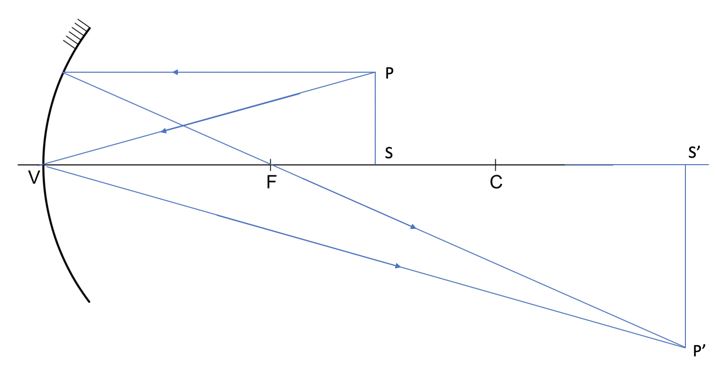
b) Como o lado QR está sobre o centro de curvatura, a sua imagem se forma embaixo do objeto (invertida), à mesma distância do vértice do espelho. Portanto, o lado Q’R’ está a 160 cm do vértice do espelho.
Para o lado PS:
- f = R/2 = 80 cm
- p = 160 – 40 = 120 cm
Aplicando a equação dos pontos conjugados, tem-se:
Dessa forma, a distância entre as imagens é d = 240 – 160 = 80 cm.