Numa feira de ciências, um estudante utilizará o disco de Maxwell (ioiô) para demonstrar o princípio da conservação da energia. A apresentação consistirá em duas etapas:
Etapa 1 - a explicação de que, à medida que o disco desce, parte de sua energia potencial gravitacional é transformada em energia cinética de translação e energia cinética de rotação;
Etapa 2 -o cálculo da energia cinética de rotação do disco no ponto mais baixo de sua trajetória, supondo o sistema conservativo.
Ao preparar a segunda etapa, ele considera a aceleração da gravidade igual a 10 m s-2 e a velocidade linear do centro de massa do disco desprezível em comparação com a velocidade angular. Em seguida, mede a altura do topo do disco em relação ao chão no ponto mais baixo de sua trajetória, obtendo da altura da haste do brinquedo.
As especificações de tamanho do brinquedo, isto é, de comprimento (C), largura (L) e altura (A), assim como da massa de seu disco de metal, foram encontradas pelo estudante no recorte de manual ilustrado a seguir.
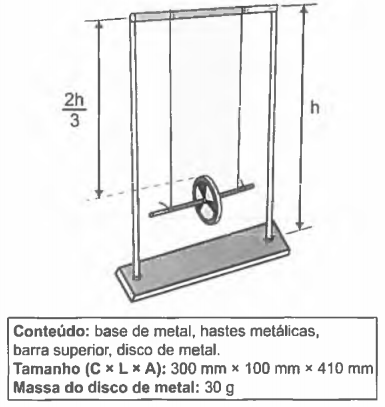
O resultado do cálculo da etapa 2, em joule, é:
Representando a situação discutida no enunciado nos pontos mais alto e mais baixo da trajetória
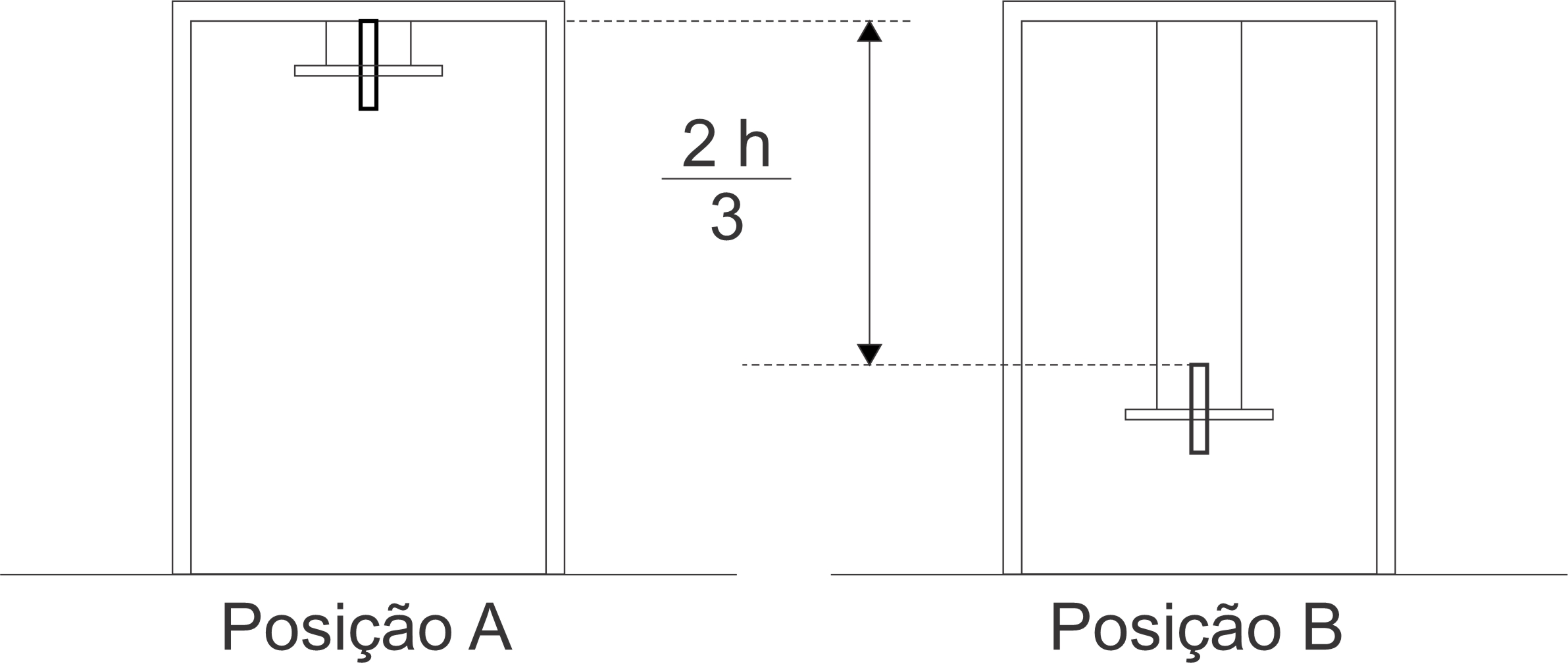
De acordo com o enunciado:
1) O sistema é conservativo;
2) A velocidade linear do centro do disco é desprezível.
Assim:
Observações
1) Para a resolução do exercício, admite-se que a haste com o disco partiu da posição "A" representada anteriormente.
2) Não é possível comparar grandezas físicas diferentes, logo, não podemos comparar a velocidade linear com a velocidade angular.