O objetivo de recipientes isolantes térmicos é minimizar as trocas de calor com o ambiente externo. Essa troca de calor é proporcional à condutividade térmica k e à área interna das faces do recipiente, bem como á diferença de temperatura entre o ambiente externo e o interior do recipiente, além de ser inversamente proporcional à espessura das faces.
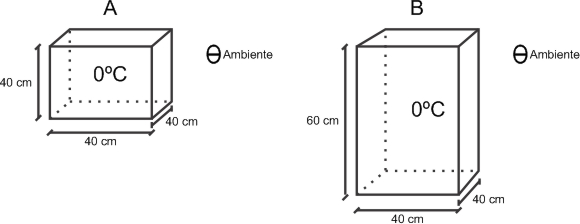
A fim de avaliar a qualidade de dois recipientes A (40 cm x 40 cm x 40 cm) e B {60 cm x 40 cm x 40 cm), de faces de mesma espessura, uma estudante compara suas condutividades térmicas kA e kB. Para isso suspende, dentro de cada recipiente, blocos idênticos de gelo a 0 °C, de modo que suas superfícies estejam em contato apenas com o ar. Após um intervalo de tempo, ela abre os recipientes enquanto ambos ainda contêm um pouco de gelo e verifica que a massa de gelo que se fundiu no recipiente B foi o dobro da que se fundiu no recipiente A.
A razão é mais próxima de
Inicialmente, pode-se determinar a área total (AT) dos recipientes A e B:
Como o calor trocado entre o ambiente e o meio interno é latente, por meio da Lei de Fourier, tem-se:
Como a massa de gelo que fundiu no recipiente B (2m) foi o dobro que fundiu em A (m), tem-se: