A figura mostra um quadro pendurado na parede do fundo de um vagão de um trem que se move com aceleração horizontal constante ah = 2,0 m/s2 . Em determinado instante, o quadro cai, deslizando em contato com a parede do vagão.
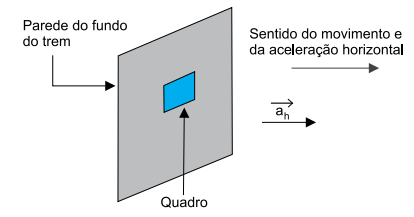
Sabendo que o coeficiente de atrito dinâmico entre as superfícies da parede e do quadro vale 0,3 e que a aceleração gravitacional vale 10 m/s2 , a aceleração vertical do quadro enquanto ele desliza pela parede é
A figura seguinte mostra a situação descrita pelo enunciado, em perfil. Nela, estão representadas as forças aplicadas no quadro (peso P, normal N e atrito dinâmico Ad), bem como as suas acelerações horizontal (ah) e vertical (av).
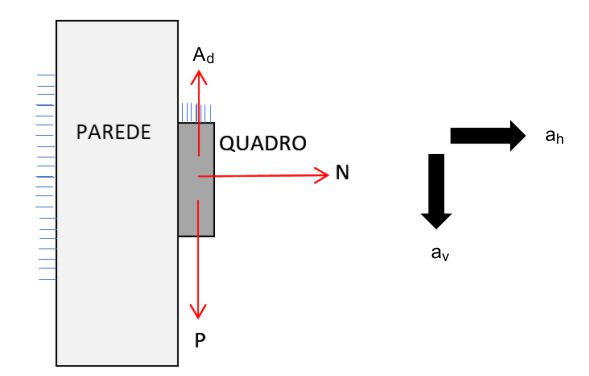
Aplicando a 2ª lei de Newton para os movimentos horizontal e vertical:
Substituindo-se (I) em (II):
Cortando-se a massa em ambos os lados da equação:
Logo, fazendo-se as devidas substituições numéricas: