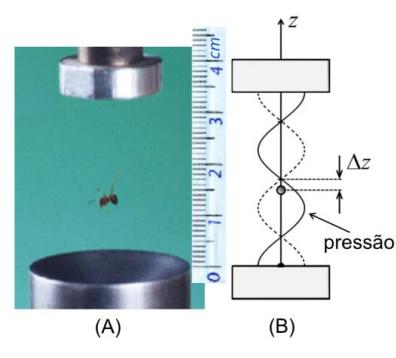
A levitação acústica consiste no emprego de ondas acústicas para exercer força sobre objetos e com isso mantê-los suspensos no ar, como a formiga representada na figura A, ou movimentá-los de forma controlada. Uma das técnicas utilizadas baseia-se na formação de ondas acústicas estacionárias entre duas placas, como ilustra a figura B, que mostra a amplitude da pressão em função da posição vertical.

a) As frequências de ressonância acústica entre duas placas, ou num tubo fechado nas duas extremidades, são dadas por fn = começar estilo tamanho matemático 14px numerador n v sobre denominador 2 L fim da fração fim do estilo, sendo L a distância entre as placas, v = 340 m/s a velocidade do som no ar, e n um número inteiro positivo e não nulo que designa o modo. Qual é a frequência do modo ilustrado na figura B?

b) A força acústica aplicada numa pequena esfera aponta sempre na direção z e no sentido do nó de pressão mais próximo. Nas proximidades de cada nó, a força acústica pode ser aproximada por Fac = −∆kz, sendo k uma constante e nó ∆z = z − znó . Ou seja, a força aponta para cima (positiva) quando a esfera está abaixo do nó (∆z negativo), e vice-versa. Se k = 6,0 ×10-2 N/m e uma esfera de massa m = 1,5 × 10-6 kg é solta a partir do repouso na posição de um nó, qual será a menor distância percorrida pela esfera até que ela volte a ficar instantaneamente em repouso? Despreze o atrito viscoso da esfera com o ar.

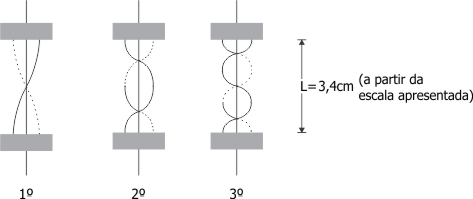
a) De acordo com o modelo apresentado, nota-se a formação de ventos nas extremidades das placas. Assim, a formação apresentada corresponde ao 3º modo, de acordo com o esquema.

Error converting from MathML to accessible text.

b) A figura a seguir ilustra a situação descrita:

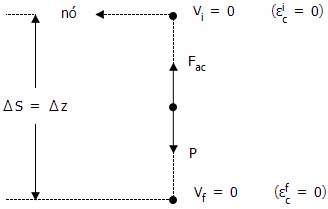
Entre as duas posições podemos aplicar o TEC.

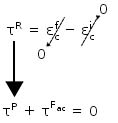
Em que:

1) começar estilo tamanho matemático 14px reto tau à potência de reto P espaço igual a espaço reto m espaço vezes espaço reto g espaço vezes espaço incremento reto z espaço parêntese esquerdo trabalho espaço motor parêntese direito fim do estilo

2) Como a força acústica apresenta comportamento semelhante ao da força elástica (F = k . x), seu trabalho é dado por:

começar estilo tamanho matemático 14px reto tau à potência de reto F com ac subscrito fim do exponencial espaço igual a espaço menos espaço numerador reto K espaço vezes espaço incremento reto z ao quadrado sobre denominador 2 fim da fração espaço parêntese esquerdo trabalho espaço resistente parêntese direito fim do estilo

Dessa forma, temos:

começar estilo tamanho matemático 14px mg riscado diagonal para baixo sobre incremento reto z fim do riscado espaço menos espaço numerador reto K espaço vezes espaço incremento reto z riscado diagonal para baixo sobre espaço em branco ao quadrado fim do riscado sobre denominador 2 fim da fração espaço igual a espaço 0 fim do estilo

Fazendo as devidas substituições numéricas:

começar estilo tamanho matemático 14px 1 vírgula 5 espaço vezes espaço 10 à potência de menos 6 fim do exponencial espaço vezes espaço 10 espaço menos espaço numerador 6 espaço vezes espaço 10 à potência de menos 2 fim do exponencial espaço vezes espaço incremento reto z sobre denominador 2 fim da fração espaço igual a espaço 0 espaço seta dupla para a direita espaço incremento reto z espaço igual a espaço 5 espaço vezes espaço 10 à potência de menos 4 espaço estreito fim do exponencial reto m espaço estreito em moldura de caixa fecha moldura fim do estilo